朴素版多重背包闫式DP分析图如下

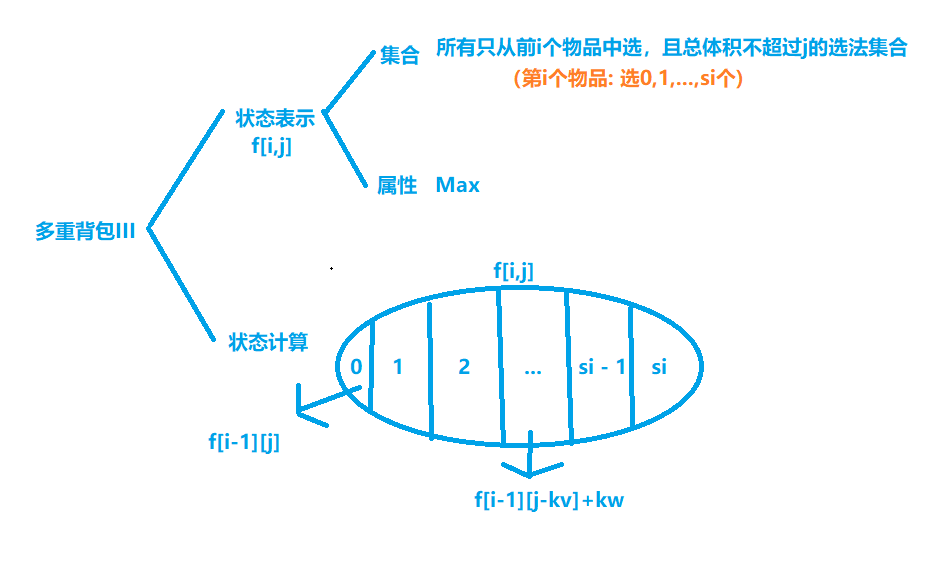
C++二维代码如下

for (int i = 1; i <= n; ++ i) {
        int v, w, s;
        cin >> v >> w >> s;
        for (int j = 0; j <= m; ++ j) 
            for (int k = 0; k <= s && k * v <= j; ++ k) 
                f[i][j] = max(f[i][j], f[i - 1][j - k * v] + k * w);
    }

C++一维代码如下

for (int i = 1; i <= n; ++ i) {
        int v, w, s;
        cin >> v >> w >> s;
        for (int j = m; j >= v; -- j) 
            for (int k = 0; k <= s && k * v <= j; ++ k) 
                f[j] = max(f[j], f[j - k * v] + k * w);
    }

通过观察朴素二维代码可发现

for (int j = 0; j <= m; ++ j) 
            for (int k = 0; k <= s && k * v <= j; ++ k) 
                f[i][j] = max(f[i][j], f[i - 1][j - k * v] + k * w);

在上述代码f[i][j] = max(f[i][j], f[i - 1][j - k * v] + k * w)中f[i - 1][j - k * v]多次重复出现，造成时间浪费；
（j : 0 ~ m, 而m / v大部分情况下存在m / v > 1，会存在不同的j和k进行j - k * v会出现相同值：j1 - k1 * v == j2 - k2 * v), 由此进行思考可考虑对其进行优化。
由于f[i][j] = max(f[i - 1][k * v] + k * w) 0 =< k <= s 对其进行展开如下图

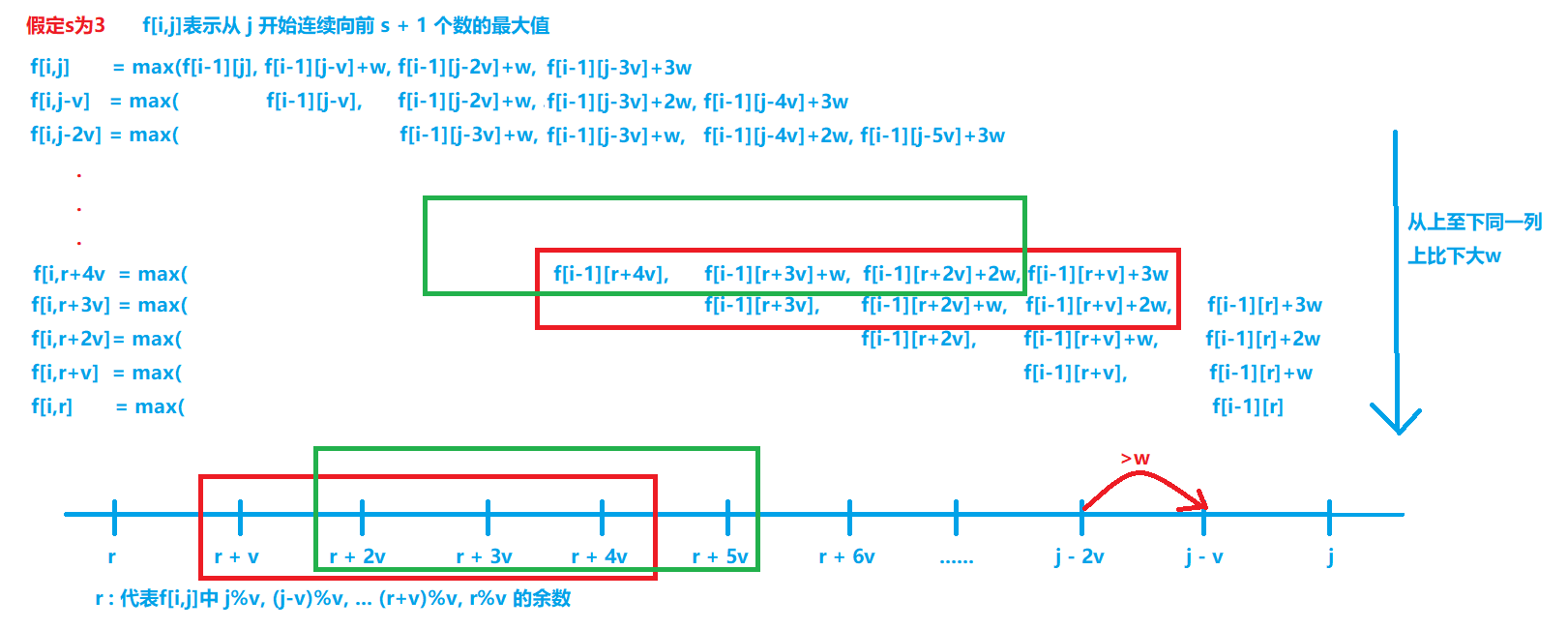
可发现f[i][j]所求随着j的上升而发生滑动，可发现适用于滑动窗口进行操作，随着j上升，选取值始终在窗口内，避免了如同朴素版多次重复计算
另外我们可以发现，在滑动窗口内，进入窗口与滑出窗口的始终余数相等满足r, r + v, r + 2v, ..., j - v, j

C++二维滑动窗口 // 辅助理解，直接使用二维会超

for (int i = 1; i <= n; ++ i) {
        int v, w, s;
        cin >> v >> w >> s;
        for (int j = 0; j < v; ++ j) {
            int hh = 0, tt = -1;
            for (int k = j; k <= m; k += v) {
                if (hh <= tt && q[hh] < k - s * v) ++ hh;
                f[i][k] = f[i-1][k];
                if (hh <= tt) f[i][k] = max(f[i][k], f[i-1][q[hh]] + (k - q[hh]) / v * w);
                while (hh <= tt && f[i-1][q[tt]] + (k - q[tt]) / v * w <= f[i-1][k]) -- tt;
                q[++tt] = k;
            }
        }
    }

C++一维滑动窗口优化代码

#include <bits/stdc++.h>

using namespace std;

const int N = 20010;

int n, m;
int f[N], g[N];
int q[N];

int main() {
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    cin >> n >> m;
    for (int i = 0; i < n; ++ i) {
        int v, w, s;
        cin >> v >> w >> s;
        memcpy(g, f, sizeof f);
        for (int j = 0; j < v; ++ j) {
            int hh = 0, tt = -1;
            for (int k = j; k <= m; k += v) {
                if (hh <= tt && q[hh] < k - s * v) ++ hh;
                if (hh <= tt) f[k] = max(f[k], g[q[hh]] + (k - q[hh]) / v * w);
                while (hh <= tt && g[q[tt]] - (q[tt] - j) / v * w <= g[k] - (k - j) / v * w) -- tt;
            //  while (hh <= tt && g[q[tt]] - q[tt] / v * w <= g[k] - k / v * w) -- tt;
            //  while (hh <= tt && g[q[tt]] + (k - q[tt]) / v * w <= g[k]) -- tt;
                q[++tt] = k;
            }
        }
    }

    cout << f[m] << "\n";

    return 0;
}

//以红色框为例
if (hh <= tt) f[k] = max(f[k], g[q[hh]] + (k - q[hh]) / v * w);
// 红色框下面三个中所找出最大值 g[q[hh]] + ?w 对其进行 "+w" 操作，与f[i-1][k]比较取最大值 
while (hh <= tt && g[q[tt]] + (k - q[tt]) / v * w <= g[k]) -- tt;
//更新红色框上面四个(s+1)个的最大值以便进行下一个j+v计算