并查集：

先按影响力降序排序，从大到小依次处理每一对冲突，处理的方法就是将两个人放到不同的监狱中，先将第一组的两个人分到两个监狱（并查集），但是这会出现一种情况：出现一对冲突，其中两个人都不在两个监狱中，这就需要预先在两个人之间建立冲突关系，在之后给出冲突后，确定这两个人所在的监狱。于是扩展出了一个域，用来存放冲突关系。

以样例为例：
第一二组冲突建立的关系，因为彼此独立，所以没有交集；

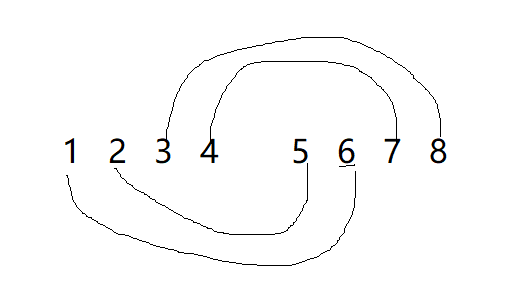
当加入第三组冲突后，将一二组联系起来了：
于是可以通过红线产生联系

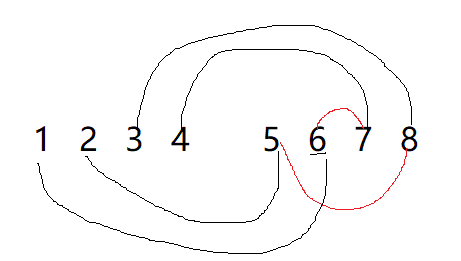
1可以通过粉色到达4，说明1、4要在一个监狱中；2可以通过褐色到达3，说明2、3要在一个监狱中。
当处理到第四组冲突时，发现2、3之间有冲突，所以输出怨气值。

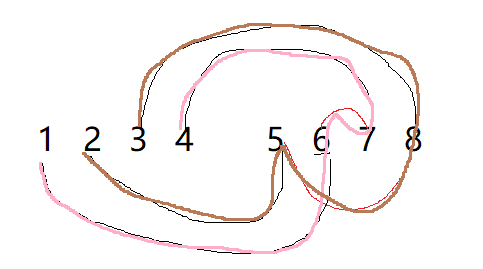
可以发现拓展出来的部分起到了中转、缓存的作用。

/*

*/

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 20010 , M = 100100;

int fa[M];
int n , m;

struct Edge{
    int a , b , c;

    bool operator < (const Edge &W)const{
        return c > W.c;
    }
}e[M];

int find(int x)
{
    return fa[x] = (fa[x] == x ? x : find(fa[x]));
}

int main()
{
    cin >> n >> m;

    for(int i = 0 ; i < m ; i++)
    {
        int a , b , c;
        cin >> a >> b >> c;
        e[i] = {a , b , c};
    }

    for(int i = 1 ; i <= 2 * n ; i++) fa[i] = i;

    sort(e , e + m);

    for(int i = 0 ; i < m ; i++)
    {
        int x = find(e[i].a) , y = find(e[i].b);
        if(x == y)//如果在同一个并查集中，说明冲突爆发
        {
            cout << e[i].c;
            return 0;
        }
        fa[x] = find(e[i].b + n);
        fa[y] = find(e[i].a + n);
    }

    cout << 0 << endl;
    return 0;
}

二分法：

二分的判断条件是能否形成二分图，如果可以形成二分图说明最大冲突不大于当前的mid，最小是0，说明所有犯人可以分到两个监狱，并且同监狱内没有边；最大是1e9.这里用染色法判断是否是二分图。

/*

*/


#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 20010 , M = 200010;

int e[M] , ne[M] , w[M] , h[N] , idx;
int color[N];
int n , m;

void add(int a , int b , int c)
{
    e[idx] = b , ne[idx] = h[a] , w[idx] = c , h[a] = idx++;
}

bool dfs(int u, int c, int mid)
{
    color[u] = c;
    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        if (w[i] <= mid) continue;
        if (color[j])
        {
            if (color[j] == c) return false;
        }
        else if (!dfs(j, 3 - c, mid)) return false;
    }

    return true;
}



bool check(int mid)
{
    memset(color , 0 , sizeof color);
    for(int i = 1 ; i <= n ; i++)
        if(!color[i])
            if(!dfs(i , 1 , mid))
                return false;

    return true;
}

int main()
{
    cin >> n >> m;

    memset(h , -1 , sizeof h);
    while(m--)
    {
        int a , b , c;
        cin >> a >> b >> c;
        add(a , b , c) , add(b , a , c);
    }

    int l = 0 , r = 1e9;
    while(l < r)
    {
        int mid = l + r >> 1;
        if(check(mid)) r = mid;
        else l = mid + 1;
    }

    cout << r << endl;
    return 0;
}