题意是寻找一个无序数组排序之后的相邻元素的最大差值。直观的思路是对数组进行排序,然后再在排序后的数组里寻找相邻元素的最大差值。
由于题目要求时间复杂度为O(n),所以我们不能用快速排序,而是用时间复杂度为O(n),空间开销较大的桶排序。
关于桶排序,可以参考这篇博客。
基本思想就是,我们先遍历一遍数组,找到整个数组的最小值和最大值Min和Max,这样,我们确定了数组内所有元素的范围,也就是从Min~Max,然后我们可以在这段范围内,
划分出若干个长度相同的区间(桶),之后我们再遍历数组,由于每个区间长度相同,且整个区间首尾确定(Min, Max),所以我们可以根据当前元素的值nums[i]计算出这个元素
应该放在哪个桶内(也就是相对于最小值Min的位移)。把所有元素都放在对应的桶内之后,按序遍历所有桶,就得到一个排好序的数组了。
这里,寻找数组最小值和最大值的时间是O(n), 遍历数组放到桶内时间也是O(n),所以总的时间复杂度就是O(n)。
不过桶排序的缺点也显而易见,空间开销大(需要额外开很多桶来存放数组元素)。
这题,还可以用鸽笼/抽屉原理进行优化。
我们可以这么想,如果每一个桶/区间内放的若干个元素之间的差值不是最终答案(即排序后相邻元素的最大差值),换句话说,任意一个桶内的两个元素之间的差值,都大于最后的答案,
那么我们只需要找相邻的桶之间的差值(也就是前一个桶的最大值和后一个桶的最小值之间的差值才有可能是最终答案)。这样的话,我们遍历所有桶的时候,就只需要看这个桶内的最小值和最大值了,因为
最终答案只和所有桶的最小值和最大值有关。
这样不是很香吗?但是我们要怎么做到任意一个桶内的元素差值不可能是最大差值呢,这里我们就要基于抽屉原理进行一顿推导了。
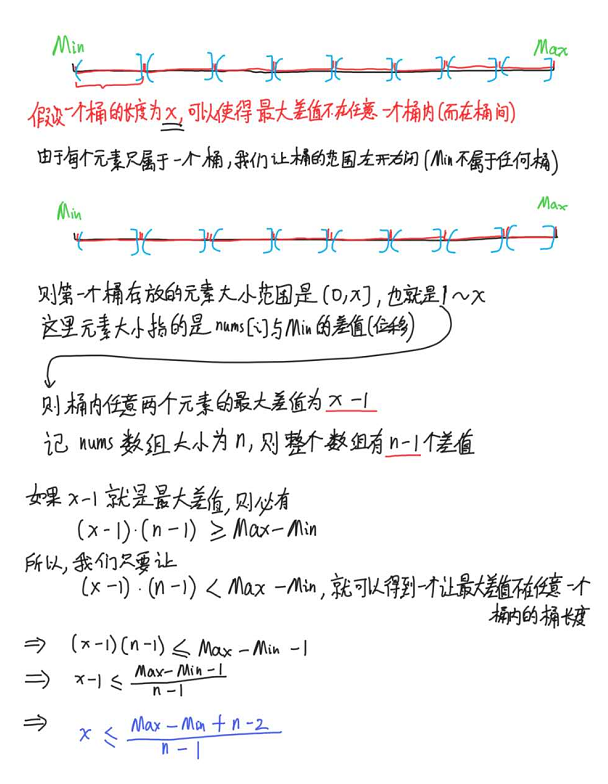
由于nums数组大小n已知,Max和Min可以一个O(n)内确定,所以我们可以求出桶长度(大小)x,使得按照这个长度划分Min~Max之间的数据为若干个桶,然后遍历一遍nums数组,把所有元素放到对应的桶内,
然后再用一个O(n)遍历所有桶,寻找每个桶的最小值和上一个桶的最大值的差值即可,(排序后的相邻元素之间的)最大差值就在这些值之间!
代码如下:
class Solution {
public:
int maximumGap(vector<int>& nums) {
struct Bucket { //每个桶都要记录最小值和最大值,以及当前桶内是否有元素(因为可能有很多桶,但并不是所有桶内都有元素)
int min, max;
bool used;
Bucket() : min(INT_MAX), max(INT_MIN), used(false) {}
};
int n = nums.size();
if(n < 2) { //如果nums数组只有一个元素或者没有元素,最大差值为0
return 0;
}
int Min = *min_element(nums.begin(), nums.end()), Max = *max_element(nums.begin(), nums.end()); //一遍O(n)寻找nums数组的最小值和最大值
if(Min == Max) { //如果最小值和最大值相等,说明nums数组中所有元素都相同,最大差值为0
return 0;
}
vector<Bucket> bucket(n - 1); //nums一个n个元素,最多n - 1个差值,所以桶的个数上限是n - 1
int len = (Max - Min + n - 2) / (n - 1); //这个len就是上面公式推导的x,也就是每个桶的长度,只要小于等于这个长度,就可以确保排序后相邻元素的最大差值不是任意一个桶内的两个元素之间的差值
for(int i = 0; i < n; ++i) { //遍历nums数组,把每个元素映射到它应该放的桶内
if(nums[i] == Min) { //桶的范围是左开右闭的,最小值Min不属于任何一个桶
continue;
}
int k = (nums[i] - Min - 1) / len; //k表示nums[i]映射到第k个桶
bucket[k].used = true; //第k个桶有元素
bucket[k].min = min(bucket[k].min, nums[i]); //更新第k个桶的最小值和最大值
bucket[k].max = max(bucket[k].max, nums[i]);
}
int res = 0;
for(int i = 0, preMax = Min; i < n - 1; ++i) { //遍历所有的桶,寻找相邻两个桶(注意是桶!)的最大差值,也就是前一个桶的最大值和第二个桶的最小值的差值。最终答案res一定是其中之一。 preMax表示上一个桶的最大值,初始赋值为最小值Min,可以理解为Min是第-1个桶的最大值
if(bucket[i].used == true) { //如果当前桶有元素,则可以更新一下res
res = max(res, bucket[i].min - preMax);
preMax = bucket[i].max; //preMax更新为这个桶的最大值,方便下一个桶计算差值
}
}
return res;
}
};

