题目描述

给你一个整数数组 nums 和一个整数 target 。

请你统计并返回 nums 中能满足其最小元素与最大元素的 和 小于或等于 target 的 非空 子序列的数目。

由于答案可能很大，请将结果对 10^9 + 7 取余后返回。

样例1

输入：nums = [3,5,6,7], target = 9
输出：4
解释：有 4 个子序列满足该条件。
[3] -> 最小元素 + 最大元素 <= target (3 + 3 <= 9)
[3,5] -> (3 + 5 <= 9)
[3,5,6] -> (3 + 6 <= 9)
[3,6] -> (3 + 6 <= 9)

样例2

输入：nums = [3,3,6,8], target = 10
输出：6
解释：有 6 个子序列满足该条件。（nums 中可以有重复数字）
[3] , [3] , [3,3], [3,6] , [3,6] , [3,3,6]

样例3

输入：nums = [2,3,3,4,6,7], target = 12
输出：61
解释：共有 63 个非空子序列，其中 2 个不满足条件（[6,7], [7]）
有效序列总数为（63 - 2 = 61）

样例4

输入：nums = [5,2,4,1,7,6,8], target = 16
输出：127
解释：所有非空子序列都满足条件 (2^7 - 1) = 127

限制

• 1 <= nums.length <= 10^5
• 1 <= nums[i] <= 10^6
• 1 <= target <= 10^6

算法1

(双指针) $O(nlogn)$

• 最小元素与最大元素的可以通过快排的方式快速找到；排序完之后可以枚举所有的最小值找对应的最大值。
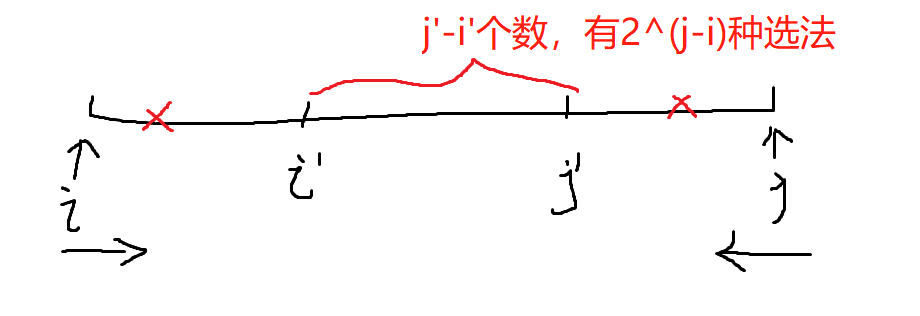
• 由于所有都是正数，i 只能从左往右走，j 只能从右往左走, 具有单调性，因此可以考虑双指针算法：对于每个 i 找到第一个符合 i' + j' <= target 的配对；
• 由于是有序的, i``前面的数都不可能有i + j <= target, 同理j’后面的数亦不符合；答案就落在[i’, j’]`的范围；
• 不管选和不选区间内其中某个数都符合要求，所以有$ 2^{j-i}$ 种选法；我们可以预处理打表所有的 $2^k$ ，不预处理的话也可以用 快速幂 下面的算法2就给出代码.

会不会有重复计数的问题？比如给的列表有重复数字, [1, 1, 1, 2, 2, 3], target = 3

• 按照上面的分析思路，排序是可以人为的给每个相等的元素进行编号, [1(1), 1(2), 1(3), 2(1), 2(2), 3]
  • 第一步：当枚举到i' == 1 的时候，对应的是i' == 1(1) 和 j' == 2(2), 此时会把答案累计一次；
  • 第二步：i' == 1(2) 并且j' == 2(2)，也会把答案累计一次；
  • ……
  • 最终，i' == 2(2) 且j' == 2(2)，整个过程结束
• 因此，每个子序列只会计算一次，所以不会出现对同一个子序列重复计数的情况。
• 注：比如 [1(1)] 和 [1(2)] 是不同的子序列，尽管它们的子序列元素一模一样。

时间复杂度

• 快排的时间复杂度是 $O(nlogn)$
• 预处理所有的 $2^{k}$, k 的最大值是和列表的长度n有关，时间复杂度是 $O(n)$
• 双指针，每个数只会遍历1次，故时间复杂度是 $O(n)$
• 故总的时间复杂度是 $O(nlogn + 2n)$

空间复杂度

• 预处理所有的 $2^k$ 需要额外的空间复杂度 $O(n)$

其他

• 双指针算法，可以参考这题AcWing 800. 数组元素的目标和
• 关于取模运算，由于是最坏情况 n == 10^5，需要预处理到 $2^{10^5}$ 会溢出int范围，而在预处理的时候提前对每一个 p[i] % MOD并不会影响最终答案取模, 它相当于： res = (res + p[j - i] % MOD % MOD % MOD % ... ) % MOD， 对p[j-i]的结果进行了 j - i 次取模，跟进行1次取模是等价的。

Go 代码

func numSubseq(nums []int, target int) int {
    const MOD int = 1e9 + 7
    sort.Ints(nums[:])
    n := len(nums)

    p := make([]int, n)
    p[0] = 1
    for i := 1; i < n; i ++ {
        p[i] = p[i - 1] * 2 % MOD
    }

    res := 0
    for i, j := 0, n - 1; i < n && j >= i; i ++ {

        for ; j >= 0 && nums[j] + nums[i] > target ; {
            j --
        }

        if j < i {
            break
        }

        res = (res + p[j - i] ) % MOD
    }

    return res
}

算法2 $O(nlog(n))$

(双指针+快速幂) $O(nlog(n))$

• 跟 算法1 不同的仅仅是，使用快速幂的方式，不预处理 $2^k$

时间复杂度

• 排序时间复杂度是 $O(nlogn)$
• 每个数只会遍历1次，故时间复杂度是 $O(n)$
• 快速幂的时间复杂度 $O(log(n))$
• 故总的时间复杂度是 $O(nlogn + log(n) + n)$

空间复杂度

• 不需要额外的空间复杂度，所以是 $O(1)$

其他

• 快速幂，可以参考这题AcWing 875. 快速幂

Go 代码

type LL int64
const MOD int = 1e9 + 7

func qmi(_a, _b int) int {
    var (
        res LL
        a LL
        b LL
        q LL
    )

    a = LL(_a)
    b = LL(_b)
    q = LL(MOD)

    res = 1 % q
    for ; b > 0 ; {

        if b & 1 == 1 {
            res = res * a % q
        }
        a = a * a % q
        b >>= 1
    }

    return int(res)
}

func numSubseq(nums []int, target int) int {
    sort.Ints(nums[:])
    n := len(nums)
    res := 0

    for i, j := 0, n - 1; i < n && j >= i; i ++ {

        for ; j >= 0 && nums[j] + nums[i] > target ; {
            j --
        }

        if j < i {
            break
        }

        res = (res + qmi(2, j - i) ) % MOD
    }

    return res
}