算法

(DP,状态机模型) $\mathcal O(n)$

从集合角度分析$DP$。

状态表示：f[i][state]

• 集合：当前已经填完了$($填满了$)$前i - 1列的格子，且第i列格子的状态为state的所有方案。
• 属性：方案数 count。

其中state是一个二进制数，共有 0、1、2、3 四种状态。
state的第i位1/0表示当前列的第i个格子是否被填上。

状态转移：

• 对于state = 0：当前列一个格子都没填的方案数，等于上一列格子填满的方案数，即$f[i][0] = f[i - 1][3]$
• 对于state = 1：有以下两种摆放方案
  
  
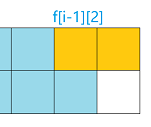
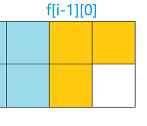
  所以$f[i][1] = f[i - 1][2] + f[i - 1][0]$
• 对于state = 2：同上，与其相反。$f[i][2] = f[i - 1][1] + f[i - 1][0]$
• 对于state = 3：有以下四种摆放方案
  
  
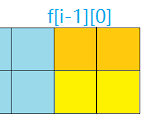
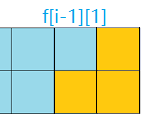
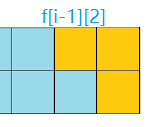
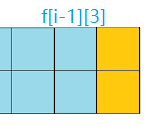
  所以$f[i][3] = f[i - 1][0] + f[i - 1][1] + f[i - 1][2] + f[i - 1][3]$

最后 $f[n][0]$ 即为答案。

时间复杂度

每次状态转移复杂度为常数级别，
一共转移 $n$ 次，
所以总的时间复杂度为 $\mathcal O(n)$。

C++ 代码

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1000005;
const int mod = 10000;

int n;
int f[N][4];

int main()
{
    scanf("%d", &n);

    f[0][3] = f[0][0] = 1;
    for (int i = 1; i <= n; i ++ )
    {
        f[i][0] = f[i - 1][3];
        f[i][1] = (f[i - 1][0] + f[i - 1][2]) % mod;
        f[i][2] = (f[i - 1][0] + f[i - 1][1]) % mod;
        f[i][3] = (f[i - 1][3] + f[i - 1][0] + f[i - 1][1] + f[i - 1][2]) % mod;
    }

    printf("%d\n",f[n][0]);

    return 0;
}