先附上我的代码,后面再附上我的解析

#include <cstring>
#include <iostream>

using namespace std;

const int N = 20;

int n;
char g[N][N];//读入图
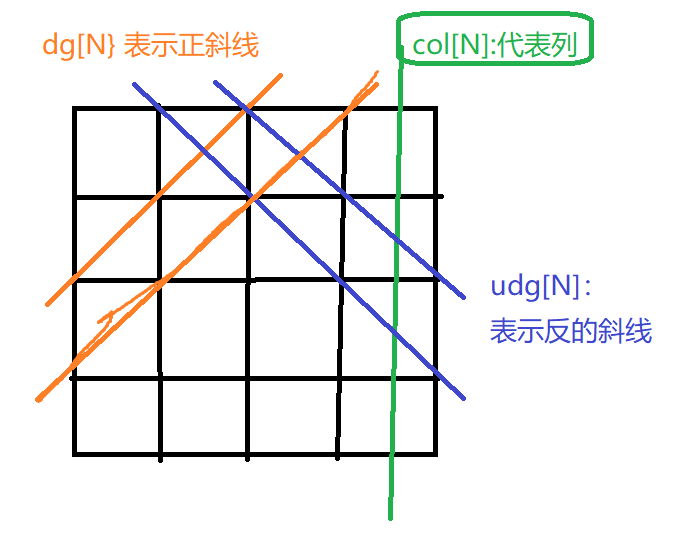
bool col[N], dg[N], udg[N];//col表示列，dg正斜线，udg反斜线

void dfs(int u){
    if (u == n){//当进行到n的时候，输出数据
        for (int i = 0; i < n; i ++ ) puts(g[i]);//输出一行的字符串
        puts("");//换行操作
        return;
    }

    for(int i = 0; i < n; i ++ )//i表示列
        if (!col[i] && !dg[n + u - i] && !udg[u + i]){
            //值为0表示当前位置不管是横着、竖着、斜着都没人，那就可以填上一个皇后
            g[u][i] = 'Q';//给这个位置安上一个皇后
            col[i] = dg[n + u - i] = udg[u + i] = true;//这个位置所在的行列斜线都被占了
            dfs(u + 1);//进行下一行
            g[u][i] = '.';//还原
            col[i] = dg[n + u - i] = udg[u + i] = false;//还原
        }
}

int main(){
    cin >> n;
    for (int i = 0; i < n; i ++ )
        for (int j = 0; j < n; j ++ )
            g[i][j] = '.';//开始的时候，每个位置都没有皇后

    dfs(0);//还是dfs

    return 0;
}

在国际象棋中，皇后有很大的本事，可以沿着横线走，也可以沿着斜线走，所以基于这一点，我们要在一个n*n的棋盘上放置n个皇后，一定不能让他们在同一行，同一列，同一斜线上，不然那还不得打起来。

对于这一题，我们应当使dfs算法是毋庸置疑的，那我们就来聊一聊该怎么使用dfs

我们知道dfs是深度优先遍历，它可以将所有的方法都给试一遍，这也就解决了题目中要求我们将所有的方案都给输出的问题。

先来介绍 一下全局变量里面开的数组

其他的地方没什么好说的，我们直接来说一下dfs函数内部的情况吧。

dfs内部只有一个要解释的，就是怎么判断某个位置所在的行、列、以及正反斜线上没有其他的皇后。
这个时候，我们进行判断就需要我们之前在全局变量里面定义的bool数组了。

col这个数组很好解释，col[i] == false就表示第i行这一行里没有皇后。
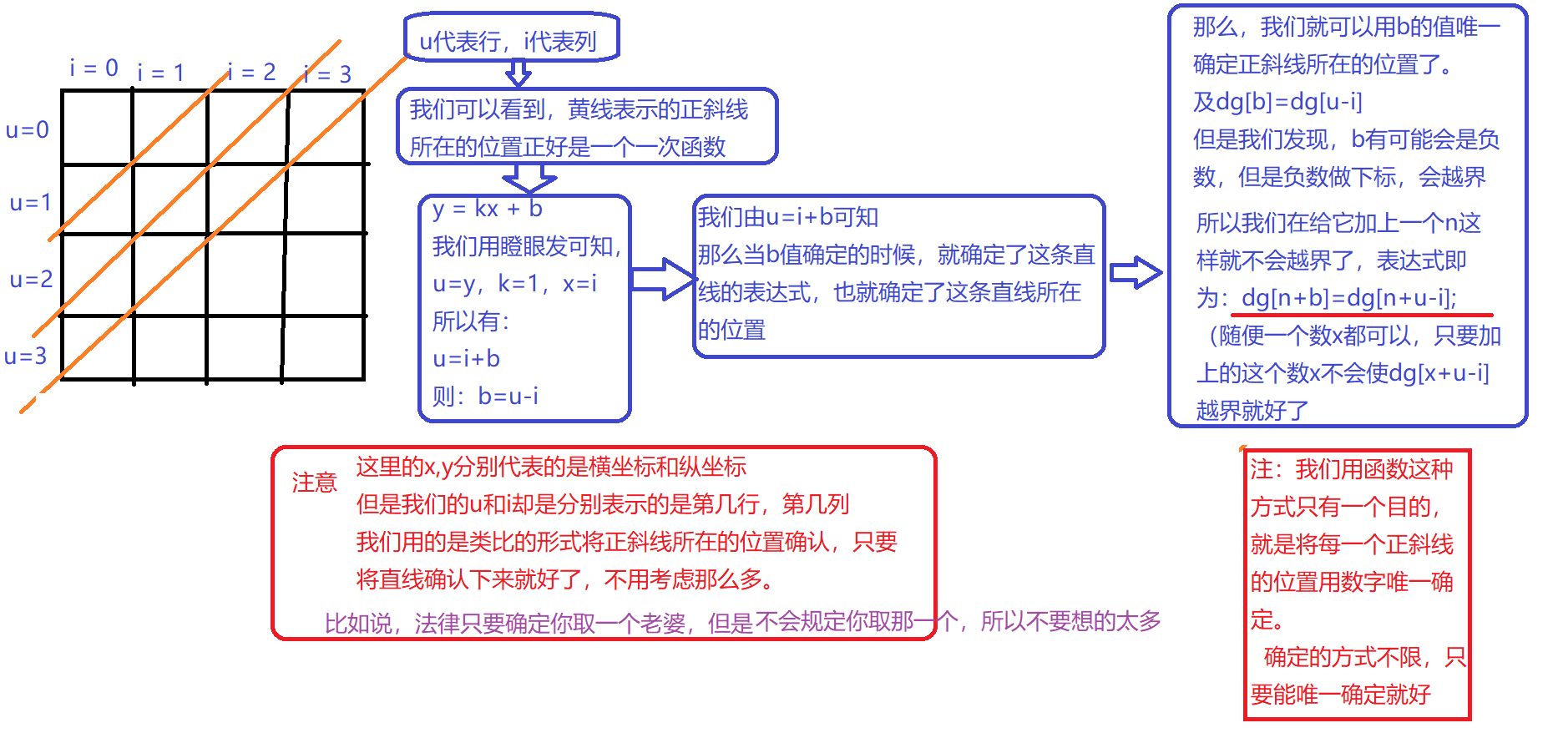
那dg这个数组表示正斜线，那dg[n+u-i]是怎么来的呢
请看下图

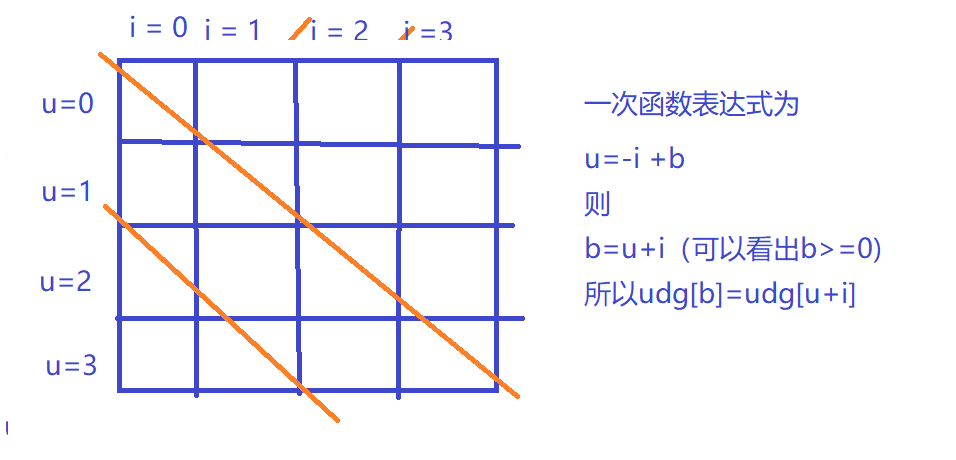
udg这个数组表示反斜线，udg[u + i}是怎么得到的呢，我们再来看一下。