题目描述

给你一个由 n 个节点（下标从 0 开始）组成的无向加权图，该图由一个描述边的列表组成，其中 edges[i] = [a, b] 表示连接节点 a 和 b 的一条无向边，且该边遍历成功的概率为 succProb[i] 。

指定两个节点分别作为起点 start 和终点 end ，请你找出从起点到终点成功概率最大的路径，并返回其成功概率。

如果不存在从 start 到 end 的路径，请 返回 0 。只要答案与标准答案的误差不超过 $1e^{-5}$ ，就会被视作正确答案。

样例1

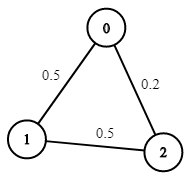
输入：n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], start = 0, end = 2
输出：0.25000
解释：从起点到终点有两条路径，其中一条的成功概率为 0.2 ，而另一条为 0.5 * 0.5 = 0.25

样例2

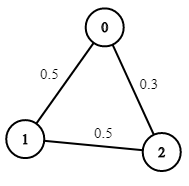
输入：n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.3], start = 0, end = 2
输出：0.30000

样例3

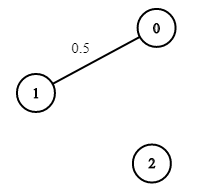
输入：n = 3, edges = [[0,1]], succProb = [0.5], start = 0, end = 2
输出：0.00000
解释：节点 0 和 节点 2 之间不存在路径

限制

• $2 \leq n \leq 10^4$
• $0 \leq start, end < n$
• $start \neq end$
• $0 \leq a, b < n$
• $a \neq b$
• $0 \leq succProb.length == edges.length \leq 2*10^4$
• $0 \leq succProb[i] \leq 1$
• 每两个节点之间最多有一条边

算法

(堆优化$Dijkstra$) $O(mlog(n))$

套了$Dijkstra$的板子求了一遍最长路

时间复杂度

建图时间复杂度$O(n)$，跑一遍$Dijkstra$时间复杂度为$O(mlog(n))$

C++ 代码

const int N = 1e4 + 10, M = 4e4 + 10;
typedef pair<double, int> PDI;

int h[N], e[M], ne[M], idx;
double w[M];
double dist[N];
bool st[N];

void add(int a, int b, double c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

class Solution {
public:
    double maxProbability(int n, vector<vector<int>>& edges, vector<double>& succProb, 
                          int start, int end) {
        memset(h, -1, sizeof h);
        idx = 0;
        for (int i = 0; i < edges.size(); i ++ ) {
            int a = edges[i][0], b = edges[i][1];
            double c = succProb[i];
            add(a, b, c), add(b, a, c);
        }

        priority_queue<PDI, vector<PDI>, less<PDI>> q;
        memset(dist, 0, sizeof dist);
        memset(st, false, sizeof st);
        dist[start] = 1;
        q.push({1, start});

        while (q.size()) {
            auto t = q.top(); q.pop();
            double d = t.first;
            int a = t.second;
            if (st[a]) continue;
            st[a] = true;

            for (int i = h[a]; ~i; i = ne[i]) {
                int j = e[i];
                if (dist[j] < d * w[i]) {
                    dist[j] = d * w[i];
                    q.push({dist[j], j});
                }
            }
        }

        return dist[end];
    }
};