题目描述

一家快递公司希望在新城市建立新的服务中心。公司统计了该城市所有客户在二维地图上的坐标，并希望能够以此为依据为新的服务中心选址：使服务中心 到所有客户的欧几里得距离的总和最小 。

给你一个数组 positions ，其中 positions[i] = [xi, yi] 表示第 $i$ 个客户在二维地图上的位置，返回到所有客户的 欧几里得距离的最小总和 。

换句话说，请你为服务中心选址，该位置的坐标 [xcentre, ycentre] 需要使下面的公式取到最小值：

$$\sum_{i = 0}^{n - 1}\sqrt{(x_{centre} - x_i) ^ 2 + (y_{centre} - y_i) ^ 2}$$

与真实值误差在 $10^{-5}$ 之内的答案将被视作正确答案。

样例1

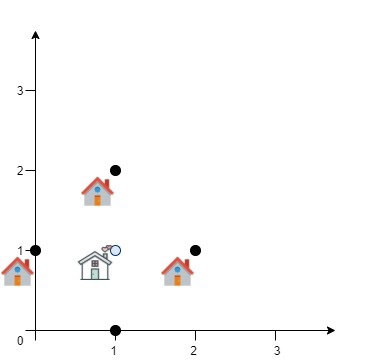
输入：positions = [[0,1],[1,0],[1,2],[2,1]]
输出：4.00000
解释：如图所示，你可以选 [xcentre, ycentre] = [1, 1] 作为新中心的位置，
这样一来到每个客户的距离就都是 1，所有距离之和为 4 ，这也是可以找到的最小值。

样例2

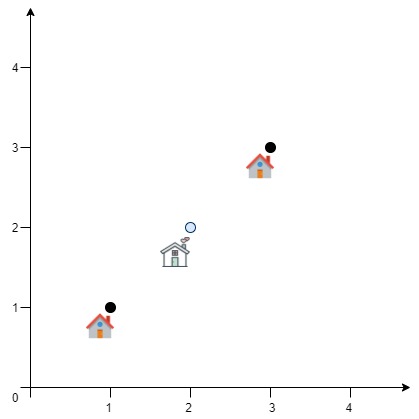
输入：positions = [[1,1],[3,3]]
输出：2.82843
解释：欧几里得距离可能的最小总和为 sqrt(2) + sqrt(2) = 2.82843

样例3

输入：positions = [[1,1]]
输出：0.00000

样例4

输入：positions = [[1,1],[0,0],[2,0]]
输出：2.73205
解释：乍一看，你可能会将中心定在 [1, 0] 并期待能够得到最小总和，但是如果选址在 [1, 0] 距离总和为 3
如果将位置选在 [1.0, 0.5773502711] ，距离总和将会变为 2.73205
当心精度问题！

样例5

输入：positions = [[0,1],[3,2],[4,5],[7,6],[8,9],[11,1],[2,12]]
输出：32.94036
解释：你可以用 [4.3460852395, 4.9813795505] 作为新中心的位置

限制

• $1 \leq positions.length \leq 50$
• $positions[i].length = 2$
• $0 \leq positions[i][0], positions[i][1] \leq 100$

算法1

(模拟退火) $O(k \times n)$

1. 初始状态时，随便选一个点作为作为起始位置，设定步长和精度不断逼近最小值对应的点
2. 精度设为$10^{-6}$足够
3. 由目标函数（到所有点的欧几里得距离之和）求得当前状态的值，根据当前时刻的值和上一时刻的值调整参数：
   • $loss$变大，需要减小步长
   • 否则，更新答案，继续以当前步长向周围扩展
4. 满足精度要求或者达到最大迭代次数则退出

时间复杂度

迭代$k$次，每次要遍历一遍所有点求距离

C++ 代码

const int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, -1, 0, 1};

class Solution {
public:
    double get_dist(vector<vector<int>>& pos, double x, double y) {
        double ret = 0;
        for (auto p: pos) {
            double a = p[0], b = p[1];
            ret += sqrt((a - x) * (a - x) + (b - y) * (b - y));
        }
        return ret;
    }

    double getMinDistSum(vector<vector<int>>& pos) {
        int n = pos.size();
        double x = pos[0][0], y = pos[0][1], d = get_dist(pos, x, y);
        double step = 10000, eps = 1e-6;
        while (step > eps) {
            int flag = 0;
            for (int i = 0; i < 4; i ++ ) {
                    double a = x + dx[i] * step, b = y + dy[i] * step;
                    double t = get_dist(pos, a, b);
                    if (t < d) {
                        x = a, y = b, d = t, flag = 1;
                        break;
                    }
            }
            if (!flag) step /= 2;
        }

        return d;
    }
};

算法2

(站在巨人的肩膀上) $O(?)$

1. scipy.optimize.minimize
2. 用到的参数只有$fun$和$x0$
3. 起始点不能乱选，比如选$pos[0]$就$gg$

时间复杂度

?

Python 代码

from scipy.optimize import minimize

class Solution:
    def getMinDistSum(self, pos: List[List[int]]) -> float:
        def get_dist(p):
            return sum([sqrt((p[0] - x) ** 2 + (p[1] - y) ** 2) for x, y in pos])
        return minimize(get_dist, [666, 666]).fun