xcy,$xhy$ $orz$

题目描述

为了随时与rainbow快速交流，Freda制造了两部传呼机。Freda和rainbow所在的地方有N座房屋、M 条双向光缆。

每条光缆连接两座房屋，传呼机发出的信号只能沿着光缆传递，并且传呼机的信号从光缆的其中一端传递到另一端需要花费t单位时间。

现在Freda要进行Q次试验，每次选取两座房屋，并想知道传呼机的信号在这两座房屋之间传递至少需要多长时间。

N座房屋通过光缆一定是连通的，并且这M条光缆有以下三类连接情况：

A：光缆不形成环，也就是光缆仅有N-1 条。
B：光缆只形成一个环，也就是光缆仅有N 条。
C：每条光缆仅在一个环中。

请你帮帮他们。

样例

in:

5 4 2
1 2 1
1 3 1
2 4 1
2 5 1
3 5
2 1

out:

3
1

PS：不喜勿喷，可出门左转看我们机房两个巨佬题解。

xcy xhy
代码：

#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e4+5;
int N,M,Q,tot,head[MAXN];
struct E {
    int next,to,val;
} e[MAXN<<3];
void add(int u,int v,int w) {
    e[++tot]=(E) {head[u],v,w};
    head[u]=tot;
}
struct A {
    int u,v,w;
    A(int u=0,int v=0,int w=0):u(u),v(v),w(w) {};
};
int dis[MAXN];
bool inQ[MAXN];
queue<int> que;
void SPFA(int S) {
    int i;
    memset(dis,0x3f,sizeof(dis));
    que.push(S);
    dis[S]=0;
    inQ[S]=true;
    while(!que.empty()) {
        int u=que.front();
        que.pop();
        inQ[u]=false;
        for(i=head[u]; i; i=e[i].next) {
            int v=e[i].to;
            if(dis[v]>dis[u]+e[i].val) {
                dis[v]=dis[u]+e[i].val;
                if(!inQ[v]) que.push(v),inQ[v]=true;
            }
        }
    }
}
stack<A> st;
int ringLen[MAXN],rcnt;
int f[MAXN],diss[MAXN];
int prework[MAXN][20];
void add2(int u,int v) {
    rcnt++;
    while(st.top().u!=u&&st.top().v!=v) {
        A a=st.top();
        st.pop();
        diss[a.u]=diss[a.v]+a.w;
        ringLen[rcnt]+=a.w;
        if(a.u!=u) f[a.u]=rcnt,prework[a.u][0]=u;
        if(a.v!=u) f[a.v]=rcnt,prework[a.v][0]=u;
    }
    A a=st.top();
    st.pop();
    diss[a.u]=diss[a.v]+a.w;
    ringLen[rcnt]+=a.w;
    prework[a.v][0]=a.u;
}
int dfn[MAXN],low[MAXN],dcnt;
void tarjan(int u,int la) {
    dfn[u]=low[u]=++dcnt;
    for(int i=head[u]; i; i=e[i].next) {
        int v=e[i].to;
        if(v==la) continue;
        if(!dfn[v]) {
            st.push(A(u,v,e[i].val));
            tarjan(v,u);
            low[u]=min(low[u],low[v]);
            if(low[v]>=dfn[u])
                add2(u,v);
        } else if(dfn[v]<low[u]) low[u]=dfn[v],st.push(A(u,v,e[i].val));
    }
}
int dpt[MAXN];
int rebuild(int u,int la) {
    dpt[u]=dpt[la]+1;
    for(int i=head[u]; i; i=e[i].next)
        rebuild(e[i].to,u);
}
inline void LCA() {
    for(int i=1; (1<<i)<=N; i++)
        for(int j=1; j<=N; j++)
            prework[j][i]=prework[prework[j][i-1]][i-1];
}

int dist(int x,int y) {
    int i;
    if(dpt[x]<dpt[y]) swap(x,y);
    int xx=dis[x],yy=dis[y];
    int maxlogn=floor(log(N)/log(2));
    for(i=maxlogn; i>=0; i--)
        if(dpt[x]-(1<<i)>=dpt[y])
            x=prework[x][i];
    if(x==y) return xx-dis[x];
    for(i=maxlogn; i>=0; i--)
        if(prework[x][i]!=prework[y][i])
            x=prework[x][i],y=prework[y][i];
    if(f[x]&&f[x]==f[y]) {
        int xyy=abs(diss[x]-diss[y]);
        int minDis=min(xyy,ringLen[f[x]]-xyy);
        return xx+yy-dis[x]-dis[y]+minDis;
    } else return xx+yy-2*dis[prework[x][0]];
}

int main() {
    int i;
    scanf("%d%d%d",&N,&M,&Q);
    for(i=1; i<=M; i++) {
        int u,v,w;
        scanf("%d%d%d",&u,&v,&w);
        add(u,v,w);
        add(v,u,w);
    }
    SPFA(1);
    tarjan(1,0);
    LCA();
    memset(head,0,sizeof(head));
    tot=0;
    for(i=2; i<=N; i++)
        add(prework[i][0],i,0);
    rebuild(1,0);
    while(Q--) {
        int x,y;
        scanf("%d%d",&x,&y);
        printf("%d\n",dist(x,y));
    }
    return 0;
}

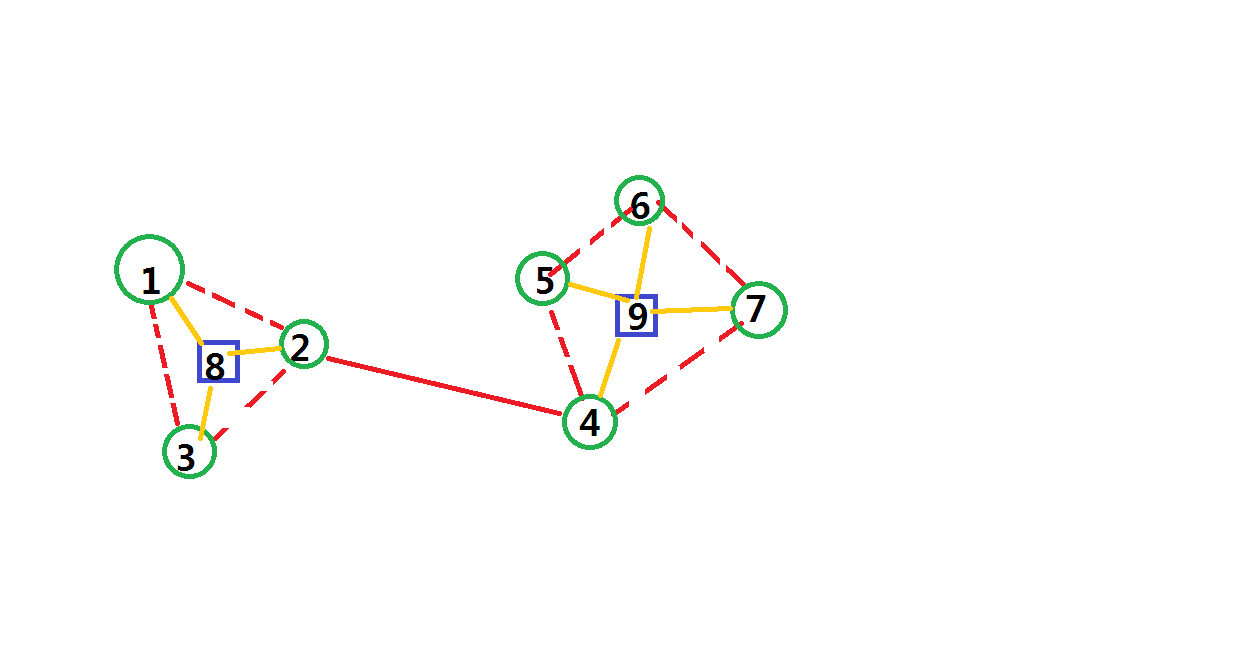
贴张自己画的圆方图