题目描述

在郊区有 $N$ 座通信基站，$P$ 条 双向 电缆，第 $i$ 条电缆连接基站Ai和Bi。

特别地，$1$ 号基站是通信公司的总站，$N$ 号基站位于一座农场中。

现在，农场主希望对通信线路进行升级，其中升级第 $i$ 条电缆需要花费Li。

电话公司正在举行优惠活动。

农产主可以指定一条从 $1$ 号基站到 $N$ 号基站的路径，并指定路径上不超过$K $条电缆，由电话公司免费提供升级服务。

农场主只需要支付在该路径上剩余的电缆中，升级价格最贵的那条电缆的花费即可。

求至少用多少钱可以完成升级。

输入格式
第1行：三个整数$N$，$P$，$K$。

第$2..P+1$行：第 $i+1$ 行包含三个整数$Ai$,$Bi$,$Li$。

输出格式
包含一个整数表示最少花费。

若$1$号基站与$N$号基站之间不存在路径，则输出”-1”。

数据范围

$0≤K<N≤1000,$
$1≤P≤10000,$
$1≤Li≤1000000$

样例

输入样例：
5 7 1
1 2 5
3 1 4
2 4 8
3 2 3
5 2 9
3 4 7
4 5 6

输出样例：
4

算法1

(二分 + 最短路)

题目中的要求是农场主可以指定不超过k个电缆的消费为0，首先，这道题可以使用二分，因为题目中问的是使得最大的值最小，所以我们可以二分最终的消费，然后对于每一次二分的消费x，根据要求，可以判断图中是否存在一条路径，这条路径上边权大于x的边小于等于k，如果满足，则说明x这个点是可以取的。

对于上面的具有二分性，这里给一个简单的证明：
如下图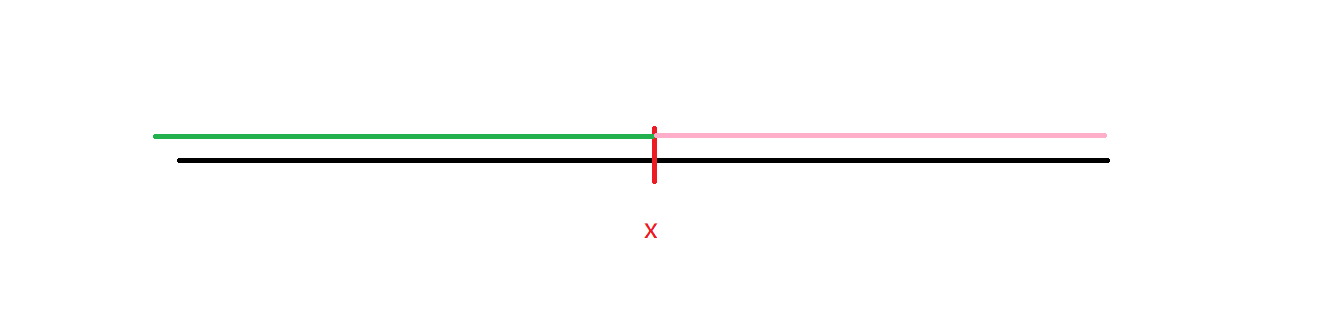
假设x这点是最终的最优解，也就是图中存在一条路径，这条路径上大于x的边权个数小于等于k，那么对于x右边的所有值都是可以满足的，而x左边的值如果满足，那么x就不是最优解了，产生矛盾，所以这道题的解具有二段性，可以使用二分来解。

时间复杂度分析：
这道题使用双端队列BFS的时间复杂度为$O(log_{2}^{L} * (n + m))$,n为点数，m为边数

需要注意的是，二分的左边界可以取0，因为如果路径总个数小于等于k，那耗费为0，右边界取1e6 + 1,因为题目中存在无解的情况，所以只要二分到了1e6 + 1，该题就是无解的。

由于边权只有0和1，所以这里可以使用双端队列BFS，也可以使用Dijkstra算法。

时间复杂度

这道题使用双端队列BFS的时间复杂度为$O(log_{2}^{L} * (n + m))$,n为点数，m为边数

参考文献

算法提高课

java 代码

import java.io.*;
import java.util.*;

class Main{
    static int N = 1010, M = 20010, max = (int)1e6 + 1, INF = 0x3f3f3f3f;
    static int[] h = new int[N];
    static int[] dist = new int[N];
    static boolean[] st = new boolean[N];
    static int[] e = new int[M];
    static int[] ne = new int[M];
    static int[] w = new int[M];
    static int n, p, k, idx;

    static void add(int a, int b, int c){
        e[idx] = b;
        w[idx] = c;
        ne[idx] = h[a];
        h[a] = idx ++;
    }

    static boolean check(int x){
        Arrays.fill(dist, INF);
        Arrays.fill(st, false);

        dist[1] = 0;
        LinkedList<Integer> q = new LinkedList<Integer>();
        q.add(1);

        while(!q.isEmpty()) {
            int t = q.removeFirst();

            if(t == n) return dist[n] <= k;

            if(st[t]) continue;
            st[t] = true;

            for(int i=h[t]; i!=-1; i=ne[i]) {
                int j = e[i];
                int c = w[i] > x ? 1 : 0;
                if(dist[j] > dist[t] + c) {
                    dist[j] = dist[t] + c;

                    if(c == 0) q.addFirst(j);
                    else q.addLast(j);
                }
            }
        }

        return false;
    }

    public static void main(String[] args) throws IOException{
        BufferedReader in = new BufferedReader(new InputStreamReader(System.in));

        Arrays.fill(h, -1);

        String[] arr = in.readLine().split(" ");
        n = Integer.parseInt(arr[0]);
        p = Integer.parseInt(arr[1]);
        k = Integer.parseInt(arr[2]);

        for(int i=0; i<p; i++){
            String[] cur = in.readLine().split(" ");
            int a = Integer.parseInt(cur[0]);
            int b = Integer.parseInt(cur[1]);
            int c = Integer.parseInt(cur[2]);

            add(a, b, c);
            add(b, a, c);
        }

        int l = 0; int r = max;
        while(l < r){
            int mid = l + r >> 1;
            if(check(mid)) r = mid;
            else l = mid + 1;
        }

        if(r == max) System.out.println(-1);
        else System.out.println(l);
    }
}

算法2

(分层图/拆点)

可以使用动态规划的思路来解决：

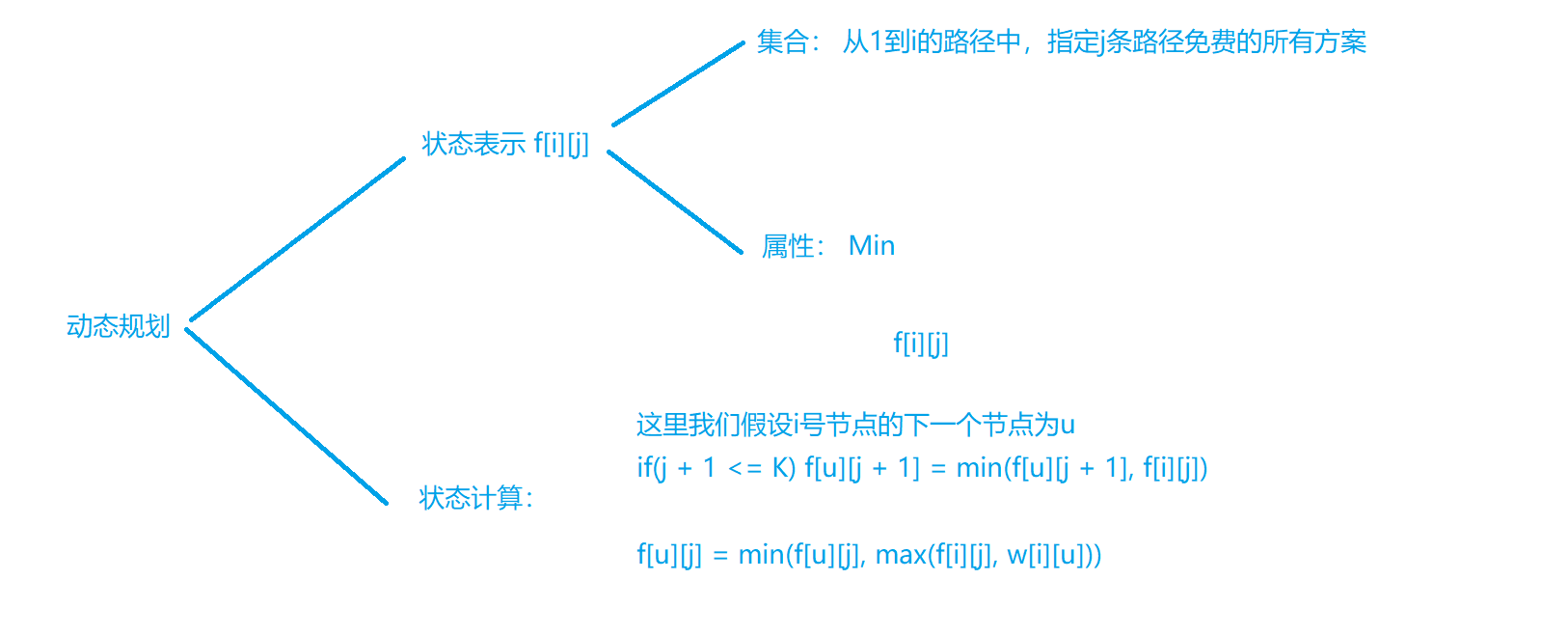
但是由于该动态规划的状态转移方程不具有拓扑结构，故这里需要使用分层图/拆点，使用最短路的求解方式实现动态规划的状态转移，最后枚举f[n][i],i = [0, k],找到一个最小值就是最终的结果，如果最小值都为正无穷，则说明无解，输出-1。

时间复杂度

这种方法的时间复杂度为$O(m * log_{2}^{n})$

参考文献

算法提高课

Java 代码

import java.io.*;
import java.util.*;

class Node implements Comparable<Node>{

    int t, k, dist;

    public Node(int t, int k, int dist){
        this.t = t;
        this.k = k;
        this.dist = dist;
    }

    @Override
    public int compareTo(Node o){
        return dist - o.dist;
    }
}

class Main{
    static int N = 1010, M = 20010, INF = 0x3f3f3f3f;
    static int[] h = new int[N];
    static int[] e = new int[M];
    static int[] ne = new int[M];
    static int[] w = new int[M];
    static int[][] dist = new int[N][N];
    static boolean[][] st = new boolean[N][N];
    static int idx, n, m, Lim;

    static void add(int a, int b, int c){
        e[idx] = b;
        w[idx] = c;
        ne[idx] = h[a];
        h[a] = idx ++;
    }

    static void Dijkstra() {
        for(int i=1; i<=n; i++) Arrays.fill(dist[i], INF);
        dist[1][0] = 0;

        PriorityQueue<Node> q = new PriorityQueue<Node>();
        q.add(new Node(1, 0, 0));

        while(!q.isEmpty()) {
            Node cur = q.poll();

            int u = cur.t;
            int k = cur.k;
            int distance = cur.dist;

            if(st[u][k]) continue;
            st[u][k] = true;

            for(int i=h[u]; i!=-1; i=ne[i]) {
                int j = e[i];

                if(k + 1 <= Lim && dist[j][k+1] > distance) {
                    dist[j][k+1] = distance;
                    q.add(new Node(j, k+1, dist[j][k+1]));
                }

                if(dist[j][k] > Math.max(distance, w[i])) {
                    dist[j][k] = Math.max(distance, w[i]);
                    q.add(new Node(j, k, dist[j][k]));
                }
            }
        }
    }

    public static void main(String[] args) throws IOException{
        BufferedReader in = new BufferedReader(new InputStreamReader(System.in));

        Arrays.fill(h, -1);

        String[] cur = in.readLine().split(" ");
        n = Integer.parseInt(cur[0]);
        m = Integer.parseInt(cur[1]);
        Lim = Integer.parseInt(cur[2]);

        while(m -- > 0){
            String[] arr = in.readLine().split(" ");
            int a = Integer.parseInt(arr[0]);
            int b = Integer.parseInt(arr[1]);
            int c = Integer.parseInt(arr[2]);

            add(a, b, c);  add(b, a, c);
        }

        Dijkstra();

        int res = INF;
        for(int i=0; i<=Lim; i++) res = Math.min(res, dist[n][i]);

        if(res == INF) System.out.println(-1);
        else System.out.println(res);
    }
}