题目描述
一家快递公司希望在新城市建立新的服务中心。公司统计了该城市所有客户在二维地图上的坐标,并希望能够以此为依据为新的服务中心选址:使服务中心 到所有客户的欧几里得距离的总和最小。
给定一个数组 positions,其中 positions[i] = [x_i, y_i] 表示第 i 个客户在二维地图上的位置,返回到所有客户的 欧几里得距离的最小总和。
换句话说,请你为服务中心选址,该位置的坐标 [x_centre, y_centre] 需要使下面的公式取到最小值:
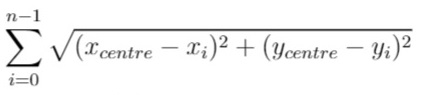
与真实值误差在 10^-5 之内的答案将被视作正确答案。
样例
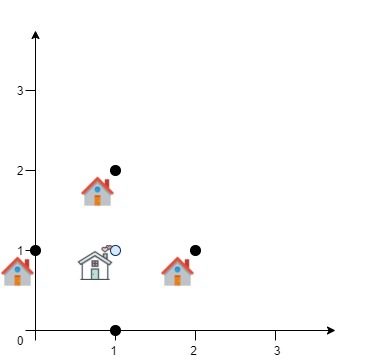
输入:positions = [[0,1],[1,0],[1,2],[2,1]]
输出:4.00000
解释:如图所示,你可以选 [xcentre, ycentre] = [1, 1] 作为新中心的位置,
这样一来到每个客户的距离就都是 1,所有距离之和为 4,这也是可以找到的最小值。
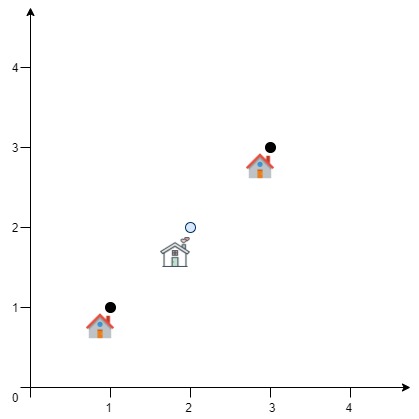
输入:positions = [[1,1],[3,3]]
输出:2.82843
解释:欧几里得距离可能的最小总和为 sqrt(2) + sqrt(2) = 2.82843
输入:positions = [[1,1]]
输出:0.00000
示例 4:
输入:positions = [[1,1],[0,0],[2,0]]
输出:2.73205
解释:乍一看,你可能会将中心定在 [1, 0] 并期待能够得到最小总和,
但是如果选址在 [1, 0] 距离总和为 3。
如果将位置选在 [1.0, 0.5773502711],距离总和将会变为 2.73205。
当心精度问题!
输入:positions = [[0,1],[3,2],[4,5],[7,6],[8,9],[11,1],[2,12]]
输出:32.94036
解释:你可以用 [4.3460852395, 4.9813795505] 作为新中心的位置。
限制
1 <= positions.length <= 50positions[i].length == 20 <= positions[i][0], positions[i][1] <= 100
算法1
(数学)
- 采用迭代法求解,初始值目标点为重心点 $y_0$。
- 通过以下公式从 $y_i$ 迭代出 $y_{i+1}$,如果两个目标点之间的变化很小,则退出迭代。
- 迭代时注意需要特殊处理目标点与给定的点重合的特殊情况。
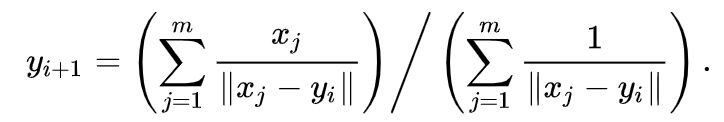
参考文献
C++ 代码
class Solution {
private:
double dist(const vector<int> &a, const vector<double> &b) {
double x = a[0] - b[0];
double y = a[1] - b[1];
return sqrt(x * x + y * y);
}
double getSum(const vector<vector<int>> &positions,
int n, const vector<double> &ans) {
double tot = 0;
for (const auto &p : positions)
tot += dist(p, ans);
return tot;
}
void weiszfeld(const vector<vector<int>> &positions,
int n, vector<double> &ans) {
vector<double> tot(2, 0.0);
double rd = 0;
const double eps = 1e-10;
for (const auto &p : positions) {
double d = dist(p, ans);
if (d < eps) continue;
rd += 1 / d;
tot[0] += p[0] / d;
tot[1] += p[1] / d;
}
if (rd < eps) return;
ans[0] = tot[0] / rd;
ans[1] = tot[1] / rd;
}
public:
double getMinDistSum(vector<vector<int>>& positions) {
int n = positions.size();
vector<double> ans(2, 0.0);
for (const auto &p : positions) {
ans[0] += p[0];
ans[1] += p[1];
}
ans[0] /= n; ans[1] /= n;
double pre = getSum(positions, n, ans);
const double eps = 1e-8;
while (1) {
weiszfeld(positions, n, ans);
double cur = getSum(positions, n, ans);
if (abs(pre - cur) < eps)
break;
pre = cur;
}
return pre;
}
};
算法2
(三分套三分)
- 我们可以分别对两个方向求偏导,发现整个决策函数是凸的,所以我们可以用三分套三分的方法找到两个维度上的总体最小值。
- 外层处理 X 维度上的,三分时找到两个三等分点
mid1和mid2,将这两个点分别代入内层 Y 维度上的三分,找到最小值,比较这两个最小值,如果calc(mid1) < calc(mid2)则令r = mid2;否则令l = mid1。
C++ 代码
class Solution {
private:
const double eps = 1e-6;
double dis(double x1, double y1, double x2, double y2) {
return sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2));
}
double calc(double x, double y, const vector<vector<int>>& positions) {
double tot = 0;
for (const auto &p : positions)
tot += dis(p[0], p[1], x, y);
return tot;
}
double calcX(double x, const vector<vector<int>>& positions) {
double l = 0, r = 100;
while (fabs(l - r) > eps) {
double len = (r - l) / 3;
double mid1 = l + len, mid2 = l + 2 * len;
if (calc(x, mid1, positions) < calc(x, mid2, positions))
r = mid2;
else
l = mid1;
}
return calc(x, l, positions);
}
public:
double getMinDistSum(vector<vector<int>>& positions) {
double l = 0, r = 100;
while (fabs(l - r) > eps) {
double len = (r - l) / 3;
double mid1 = l + len, mid2 = l + 2 * len;
if (calcX(mid1, positions) < calcX(mid2, positions))
r = mid2;
else
l = mid1;
}
return calcX(l, positions);
}
};

