题目描述：

给Alice一个带有N个数字的数组A [1…N]。
现在，Alice想通过参数K按照以下规则构建数组B：
最初，数组B为空。考虑数组A中的每个间隔。如果此间隔的长度小于K，则忽略此间隔。否则，在此间隔中找到第K个最大数字，并将此数字添加到数组B中。
实际上，Alice不在乎数组B中的每个元素。她只想知道数组B中的第M个最大元素。请帮助她找到这个数。

输入描述：

第一行是测试用例的数量。
对于每一个测试的情况下，第一行包含三个正数$N（1≤N≤10^5）; K（1≤K≤N）; M。$
第二行包含N个数甲$Ai（1≤Ai≤10^9）$。
保证M不大于数组B的长度。

输出描述：

对于每个测试用例，输出一行包含数组B中第M个最大元素的一行。

Sample Input

2
5 3 2
2 3 1 5 4
3 3 1
5 8 2

Sample Output

3
2

题解

• 我们从下标为1的位置开始记录a[i] >= x的个数，当恰好有k个数大于等于x了(假设到下标i的时候恰好有k个数大于等于x了)，那么区间[1,i]内一定能够作为一个区间，找到一个第K大数大于等于x。

• 那么我保持前面下标为1不动，向后一个一个的扩展，也一定能找到一个第K大的数大于等于x。

• 即在区间[1,i]，[1,i+1],[1,i+2],[1,i+3]…[1,n]，这些区间都可以找到第K大的数大于等于x，即此时共有n-i+1个区间其第K大的数大于等于x。

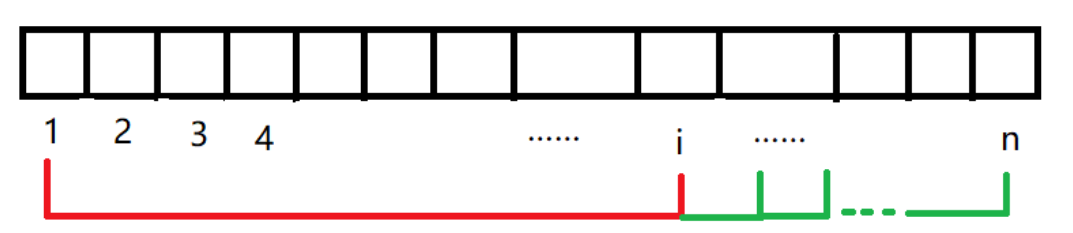
那么只有这些吗?

• 我们定义下标j，让j从头开始，即从1开始，往后移动，如果a[j] < x,那么这个数a[j]对于第K大的数是否大于等于x没有影响，因为它比x小，所以这个时候我们可以去掉它。
• j往后移动一格，这样相当于起点变了，但是终点还是i，所以满足条件的区间还是[j,i],[j,i+1],[j,i+1]…[j,n]，而且区间[j,i],[j,i+1],[j,i+1]…[j,n]中仍然有k个大于等于x的数，所以我们区间个数还是加上n-i+1，这个过程while循环即可，直到a[j] >= x停止，否则可以一直进行。

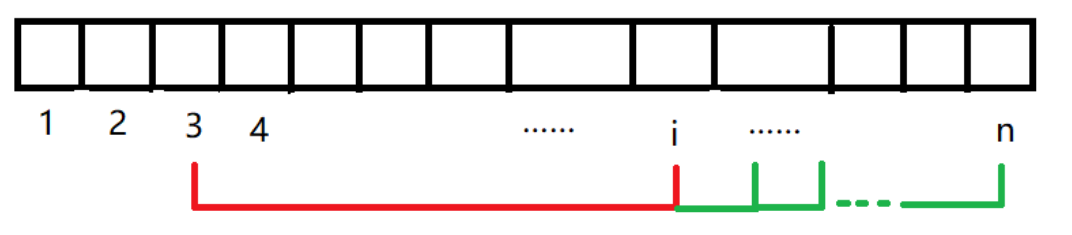
如果这个时候a[j]是一个大于等于x的数呢？

• a[j] >= x，此时我们停止循环。
• 我们要去掉这个数，从下一个开始，因此循环停止后，j++。
• 大于等于x的个数要减1，这个时候，我们就得变化终点i了，i往后寻找到又一个第K大的数大于等于x的位置，重复上面的操作即可。

这样我们就可以求得第K大数大于等于x的区间一共有多少个。
如果个数大于等于M个说明我们枚举的x小了，否则我们枚举的x大了。

const int N=1e5+10;
int a[N];
int b[N];
int n,k;
LL m;

bool check(int x)
{
    LL res=0;
    int cnt=0;
    for(int i=1,j=1;i<=n;i++)
    {
        if(a[i] >= x) cnt++;
        if(cnt == k)
        {
            res+=n-i+1;
            while(a[j] < x)
            {
                res+=n-i+1;
                j++;
            }
            cnt--;
            j++;
        }
    }
   // cout<<"---"<<x<<' '<<res<<endl;
    if(res >= m) return true;
    else return false;
}

int main()
{
    int T;
    cin>>T;
    while(T--)
    {
        cin>>n>>k>>m;

        for(int i=1;i<=n;i++) cin>>a[i],b[i]=a[i];

        sort(b+1,b+n+1);

        int l=1,r=n;
        while(l<r)
        {
            int mid=l+r+1>>1;
            if(check(b[mid])) l=mid;
            else r=mid-1;
        }

        cout<<b[l]<<endl;

    }

    //system("pause");
}