问题描述

Suppose an array sorted in ascending order is rotated at some pivot unknown to you beforehand.

(i.e., [0,1,2,4,5,6,7] might become [4,5,6,7,0,1,2]).

You are given a target value to search. If found in the array return its index, otherwise return -1.

You may assume no duplicate exists in the array.

Your algorithm’s runtime complexity must be in the order of O(log n).

在旋转数组中找到目标值，若不存在，则返回-1。

假设数组中不包含重复的数字，时间复杂度要求是O(log n)。

举个例子：

Input: nums = [4,5,6,7,0,1,2], target = 0
Output: 4

解法1

Thanks [Y总]

先来看下示意图：

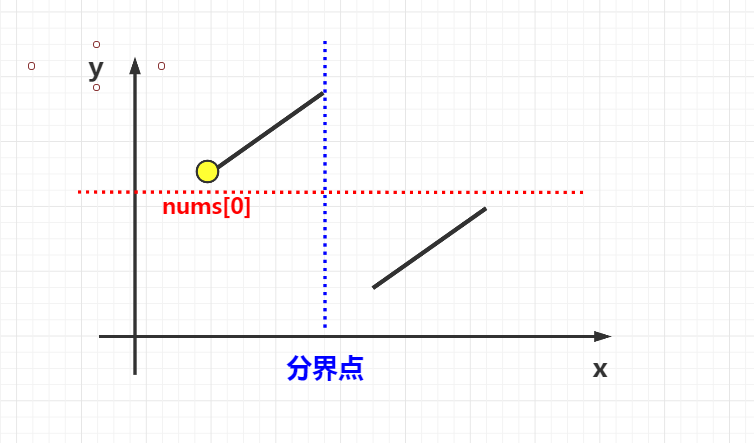
首先，我们需要求出蓝色分界线的下标pivot。

为什么？

一旦求出分界点，我们就知道了两段有序数组的分界点，就可以对某一段进行二分查找。

那么，我们如何求出pivot？

对于这两段区间，你会发现一个性质：

左边区间内所有的点都大于等于nums[0]，而右边区间内所有的点都小于nums[0]。

所以，我们可以这样找到分界点pivot：

int n = nums.length;
int l = 0, r = n - 1;
while (l < r){
    int mid = l + r + 1 >> 1;
    if (nums[mid] >= nums[0]) l = mid;
    else r = mid - 1;
}

接下来的一个问题就是，我们如何确定应该在哪段升序区间进行二分查找？

令目标值target与nums[0]进行比较，若大于等于，说明是左边的，否则右边：

if (target >= nums[0]){
    // left
    l = 0;
} else {
    // right
    l = r + 1;
    r = n - 1;
}

最后，问题就变成了在一段升序数组中找某个值~

来看下完整实现：

class Solution {
    public int search(int[] nums, int target) {

        int n = nums.length;
        if (n == 0) return -1;

        // 1. 确定左右分界点
        int l = 0, r = n - 1;
        while (l < r){
            int mid = l + r + 1>> 1;
            if (nums[mid] >= nums[0]) l = mid;
            else r = mid - 1;
        }

        // 2. 确定升序区间
        if (target >= nums[0]){
            // left
            l = 0;
        } else {
            // right
            l = r + 1;
            r = n - 1;
        }

        // 3. 找目标值
        while (l < r){
            int mid = l + r >> 1;
            if (nums[mid] >= target) r = mid;
            else l = mid + 1;
        }

        return nums[r] == target ? r : -1;
    }
}

Enjoy it !