题目描述

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

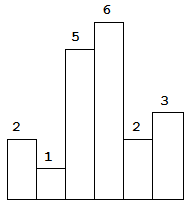
以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3]。

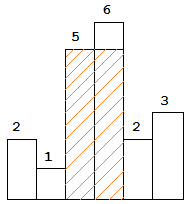
图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。

样例

输入: [2,1,5,6,2,3]
输出: 10

算法分析

单调栈

对于每个柱子i，找到左边第一个比它小的柱子的位置left[i]，和找到右边第一个比它小的柱子的位置right[i]，(right[i] - left[i] - 1) * heights[i]是当前柱子所能找到的最大的矩形面积

如何找到左边第一个比它小的柱子的位置？

维护一个单调递增的栈，当枚举到当前柱子时，若栈顶元素的值比它大，则将栈顶元素pop出，直到栈顶元素的值小于等于它为止，则栈顶元素记录的就是左边第一个比它小的元素的位置，最后把当前元素加入到栈中，继续维护栈的单调性

时间复杂度 $O(n)$

Java 代码

class Solution {
    public int largestRectangleArea(int[] heights) {
        int n = heights.length;
        int[] stk = new int[n + 10];
        int tt = 0;
        int[] left = new int[n + 10];
        for(int i = 0;i < n;i ++)
        {
            while(tt != 0 && heights[stk[tt]] >= heights[i]) tt --;
            if(tt == 0) left[i] = -1;
            else left[i] = stk[tt];
            stk[++ tt] = i;
        }

        tt = 0;
        int[] right = new int[n + 10];
        for(int i = n - 1;i >= 0;i --)
        {
            while(tt != 0 && heights[stk[tt]] >= heights[i]) tt --;
            if(tt == 0) right[i] = n;
            else right[i] = stk[tt];
            stk[++ tt] = i;
        }
        int ans = 0;
        for(int i = 0;i < n;i ++)
        {
            ans = Math.max(ans,(right[i] - left[i] - 1) * heights[i]);
        }
        return ans;
    }
}