idea

题目描述

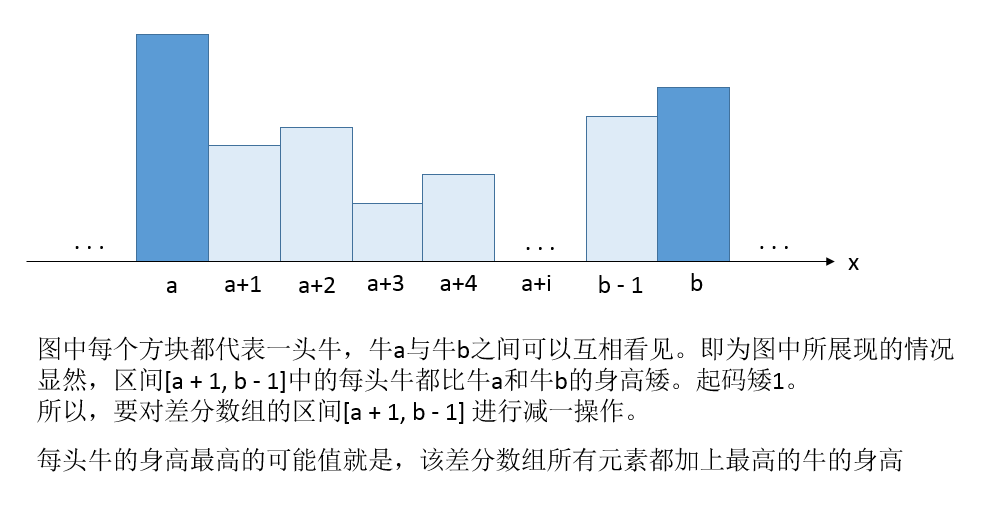
有 N 头牛站成一行，被编队为1、2、3…N，每头牛的身高都为整数。

当且仅当两头牛中间的牛身高都比它们矮时，两头牛方可看到对方。

现在，我们只知道其中最高的牛是第 P 头，它的身高是 H ，剩余牛的身高未知。

但是，我们还知道这群牛之中存在着 M 对关系，每对关系都指明了某两头牛 A 和 B 可以相互看见。

求每头牛的身高的最大可能值是多少。

输入格式
第一行输入整数N,P,H,M，数据用空格隔开。

接下来M行，每行输出两个整数 A 和 B ，代表牛 A 和牛 B 可以相互看见，数据用空格隔开。

输出格式
一共输出 N 行数据，每行输出一个整数。

第 i 行输出的整数代表第 i 头牛可能的最大身高。

数据范围
1≤N≤10000,
1≤H≤1000000,
1≤A,B≤10000,
0≤M≤10000

输入样例：

9 3 5 5
1 3
5 3
4 3
3 7
9 8

输出样例：

5
4
5
3
4
4
5
5
5

注意：此题中给出的关系对可能存在重复

算法1

C++ 代码

#include <iostream>
#include <map>
using namespace std;
const int N = 1e5 + 10;
map<pair<int, int>, bool> existed;
int d[N];

void insert(int l, int r, int c) {
    d[l] += c;
    d[r + 1] -= c;
}

int main() {
    int n, p, h, m;
    cin >> n >> p >> h >> m;
    d[1] = h; // 初始化差分数组，牛的身高均为h
    // 输入m对牛可相互看见的视觉关系
    while(m--) {
        int a, c; 
        cin >> a >> c;
        if(a > c) swap(a, c);
        if(existed[{a, c}]) continue;
        existed[{a, c}] = true;
        insert(a + 1, c - 1, -1); // 牛a与牛c之间的都是那一群隐身的牛b!
    }
    // 差分转换成前缀和，即为结果
    for(int i = 1; i <= n; i++) {
        d[i] += d[i - 1];
        cout << d[i] << endl;
    }
    return 0;
}