题目描述
给你一棵树(即,一个连通的无环无向图),
这棵树由编号从 0 到 n - 1 的 n 个节点组成,且恰好有 n - 1 条 edges 。
树的根节点为节点 0 ,树上的每一个节点都有一个标签,
也就是字符串 labels 中的一个小写字符(编号为 i 的 节点的标签就是 labels[i] )
边数组 edges 以 edges[i] = [ai, bi] 的形式给出,该格式表示节点 ai 和 bi 之间存在一条边。
返回一个大小为 n 的数组,其中 ans[i] 表示第 i 个节点的子树中与节点 i 标签相同的节点数。
树 T 中的子树是由 T 中的某个节点及其所有后代节点组成的树。
示例1
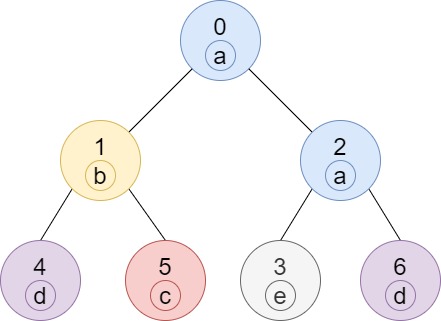
输入:n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], labels = "abaedcd"
输出:[2,1,1,1,1,1,1]
解释:节点 0 的标签为 'a' ,以 'a' 为根节点的子树中,节点 2 的标签也是 'a' ,
因此答案为 2 。注意树中的每个节点都是这棵子树的一部分。
节点 1 的标签为 'b' ,节点 1 的子树包含节点 1、4 和 5,
但是节点 4、5 的标签与节点 1 不同,故而答案为 1(即,该节点本身)。
示例2
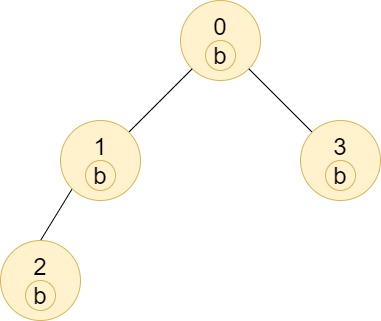
输入:n = 4, edges = [[0,1],[1,2],[0,3]], labels = "bbbb"
输出:[4,2,1,1]
解释:节点 2 的子树中只有节点 2 ,所以答案为 1 。
节点 3 的子树中只有节点 3 ,所以答案为 1 。
节点 1 的子树中包含节点 1 和 2 ,标签都是 'b' ,因此答案为 2 。
节点 0 的子树中包含节点 0、1、2 和 3,标签都是 'b',因此答案为 4 。
示例 3:
输入:n = 5, edges = [[0,1],[0,2],[1,3],[0,4]], labels = "aabab"
输出:[3,2,1,1,1]
示例 4:
输入:n = 6, edges = [[0,1],[0,2],[1,3],[3,4],[4,5]], labels = "cbabaa"
输出:[1,2,1,1,2,1]
示例 5:
输入:n = 7, edges = [[0,1],[1,2],[2,3],[3,4],[4,5],[5,6]], labels = "aaabaaa"
输出:[6,5,4,1,3,2,1]
提示:
1 <= n <= 10^5
edges.length == n - 1
edges[i].length == 2
0 <= ai, bi < n
ai != bi
labels.length == n
labels 仅由小写英文字母组成
算法1
开始考虑使用并查集,沿着父亲链向上回溯即可。
后来发现数据中挺多坑的,点和点时无向,无法判断边的两点那个是父亲那个是儿子。
最后发现解决办法是暴力遍历,使用哈希记录子树中包含的字母,然后层层向上传递
C++ 代码
class Solution {
public:
int vis[100010];
int mm[100010][26];
vector<vector<int>> g;
vector<int> ans;
void dfs(int idx, const string& labels)
{
vis[idx] = 1; mm[idx][(int)labels[idx] - 'a']++;
for (int i = 0; i < g[idx].size(); i++) {
int x = g[idx][i];
if (vis[x] == 1) continue;
dfs(x, labels);
for (int i = 0; i < 26; i++) {
mm[idx][i] += mm[x][i];
}
}
}
vector<int> countSubTrees(int n, vector<vector<int>>& edges, string labels)
{
g.resize(n, vector<int>());
ans.resize(n);
memset(mm, 0, sizeof mm);
for (int i = 0; i < edges.size(); i++) {
int a = edges[i][0];
int b = edges[i][1];
g[a].push_back(b);
g[b].push_back(a);
}
vis[0] = 1; mm[0][(int)labels[0] - 'a'] = 1;
for (int i = 0; i < g[0].size(); i++) {
int x = g[0][i];
dfs(x, labels);
for (int i = 0; i < 26; i++) {
mm[0][i] += mm[x][i];
}
}
for (int i = 0; i < n; i++) {
int chIdx = labels[i] -'a';
ans[i] += mm[i][chIdx];
}
return ans;
}
};

