题目描述
设一个n个节点的二叉树tree的中序遍历为(1,2,3,…,n),其中数字1,2,3,…,n为节点编号。
每个节点都有一个分数(均为正整数),记第i个节点的分数为di,tree及它的每个子树都有一个加分,任一棵子树subtree(也包含tree本身)的加分计算方法如下:
subtree的左子树的加分 × subtree的右子树的加分 + subtree的根的分数
若某个子树为空,规定其加分为1。叶子的加分就是叶节点本身的分数,不考虑它的空子树。
试求一棵符合中序遍历为(1,2,3,…,n)且加分最高的二叉树tree。
要求输出:
(1)tree的最高加分
(2)tree的前序遍历
输入格式
第1行:一个整数n,为节点个数。
第2行:n个用空格隔开的整数,为每个节点的分数(0<分数<100)。
输出格式
第1行:一个整数,为最高加分(结果不会超过4,000,000,000)。
第2行:n个用空格隔开的整数,为该树的前序遍历。如果存在多种方案,则输出字典序最小的方案。
样例
输入样例
5
5 7 1 2 10
输出样例
145
3 1 2 4 5
算法1
(区间DP举) $O(n^3)$
首先分析题面,得到题面所要求的是什么,此题要求我们求出一个最大的加分。在仔细看一下题,我们需要知道什么是先序遍历和中序遍历。
1.先序遍历:根–>左子树–>右子树
2.中序遍历:左子树–>根–>右子树
了解到了遍历情况后,我们就可以根据这些遍历的特点来分析题面。
因为中序遍历为左根右,所以,我们可以得到y总画的这个图
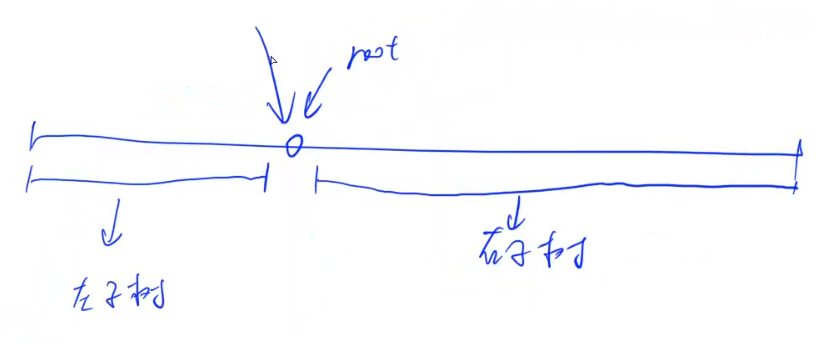
由此图可以发现,我们在找到一个根节点时,此根节点的左子树就是[1,root-1],右子树就是[root+1,n]。根据这个我们就可以联想到区间DP。
再根据闫氏DP分析法来看
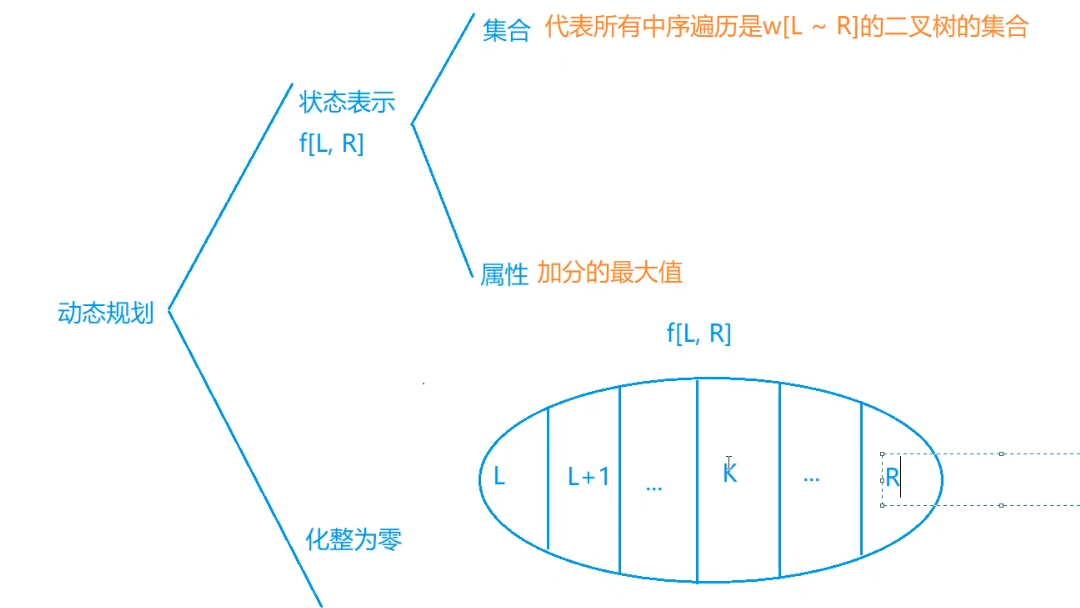
我们根据题目可知我们要求得属性为max,我们定义一个数组f[l][r]为在[l,r]之间的最大加分值。
所以,我们也就得到了状态转移方程f[i][j]=max(f[i][k - 1]*f[k + 1][j]+a[k])k为根节点。所以就在枚举区间的过程中进行状态转移即可。
此题还有一个难点就是需要记录一下路径,所以我们可以开一个path[l][r],为在[l,r]上的根节点。所以,我们就可以根据我们记录的根节点进行递归求先序遍历,输出即可。
-------图片来源于y总讲解视频
参考文献
敬请观看y总讲解视频或题解
C++ 代码
#include<bits/stdc++.h>
using namespace std;
int a[50],f[50][50],g[50][50];
void shuchu(int l,int r)
{
if(l>r)
return ;
cout<<g[l][r]<<' ';
shuchu(l,g[l][r]-1);
shuchu(g[l][r]+1,r);
}
int main()
{
int n;
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a[i];
}
for(int len=1;len<=n;len++)
{
for(int l=1;l+len-1<=n;l++)
{
int r=l+len-1;
if(len==1)
{
f[l][r]=a[l];
g[l][r]=l;
}
else
{
for(int k=l;k<=r;k++)
{
int left1,right1,fen;
if(k==l)
{
left1=1;
}
else
{
left1=f[l][k-1];
}
if(r==k)
{
right1=1;
}
else
{
right1=f[k+1][r];
}
fen=left1*right1+a[k];
if(f[l][r]<fen)
{
f[l][r]=fen;
g[l][r]=k;
}
}
}
}
}
cout<<f[1][n]<<endl;
shuchu(1,n);
}



 回复
回复

