题目描述
近来,一种新的传染病肆虐全球。
蓬莱国也发现了零星感染者,为防止该病在蓬莱国大范围流行,该国政府决定不惜一切代价控制传染病的蔓延。
不幸的是,由于人们尚未完全认识这种传染病,难以准确判别病毒携带者,更没有研制出疫苗以保护易感人群。
于是,蓬莱国的疾病控制中心决定采取切断传播途径的方法控制疾病传播。
经过 WHO(世界卫生组织)以及全球各国科研部门的努力,这种新兴传染病的传播途径和控制方法已经研究清楚,剩下的任务就是由你协助蓬莱国疾控中心制定一个有效的控制办法。
研究表明,这种传染病的传播具有两种很特殊的性质:
第一是它的传播途径是树型的,一个人X只可能被某个特定的人Y感染,只要Y不得病,或者是XY之间的传播途径被切断,则X就不会得病。
第二是,这种疾病的传播有周期性,在一个疾病传播周期之内,传染病将只会感染一代患者,而不会再传播给下一代。
这些性质大大减轻了蓬莱国疾病防控的压力,并且他们已经得到了国内部分易感人群的潜在传播途径图(一棵树)。
但是,麻烦还没有结束。
由于蓬莱国疾控中心人手不够,同时也缺乏强大的技术,以致他们在一个疾病传播周期内,只能设法切断一条传播途径,而没有被控制的传播途径就会引起更多的易感人群被感染(也就是与当前已经被感染的人有传播途径相连,且连接途径没有被切断的人群)。
当不可能有健康人被感染时,疾病就中止传播。
所以,蓬莱国疾控中心要制定出一个切断传播途径的顺序,以使尽量少的人被感染。
你的程序要针对给定的树,找出合适的切断顺序。
输入格式
第一行是两个整数n和p。
接下来p行,每一行有2个整数i和j,表示节点i和j间有边相连(意即,第i人和第j人之间有传播途径相连)。
其中节点1是已经被感染的患者。
输出格式
输出共一行,一个整数表示总共被感染的人数。
样例
输入样例
7 6
1 2
1 3
2 4
2 5
3 6
3 7
输出样例
3
算法1
(DFS) $O(2^n)$
首先分析一下题面,可以得到现在有一个传染病,每次会传染与它相邻的节点,每次可以切断一条传染路径,问剩下有多少节点。
首先会想到的是贪心做法,但贪心做法是不对的,根据y总提供的反例可知
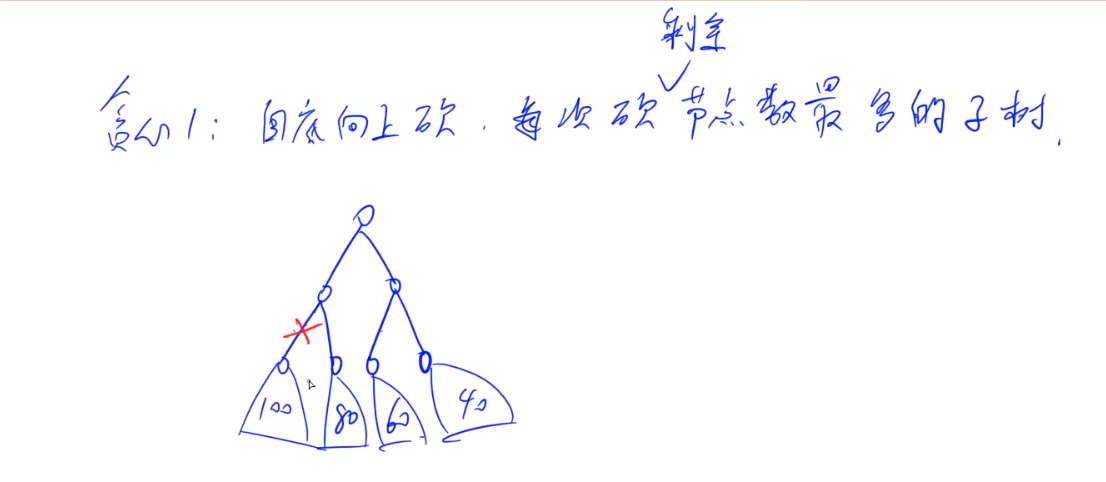
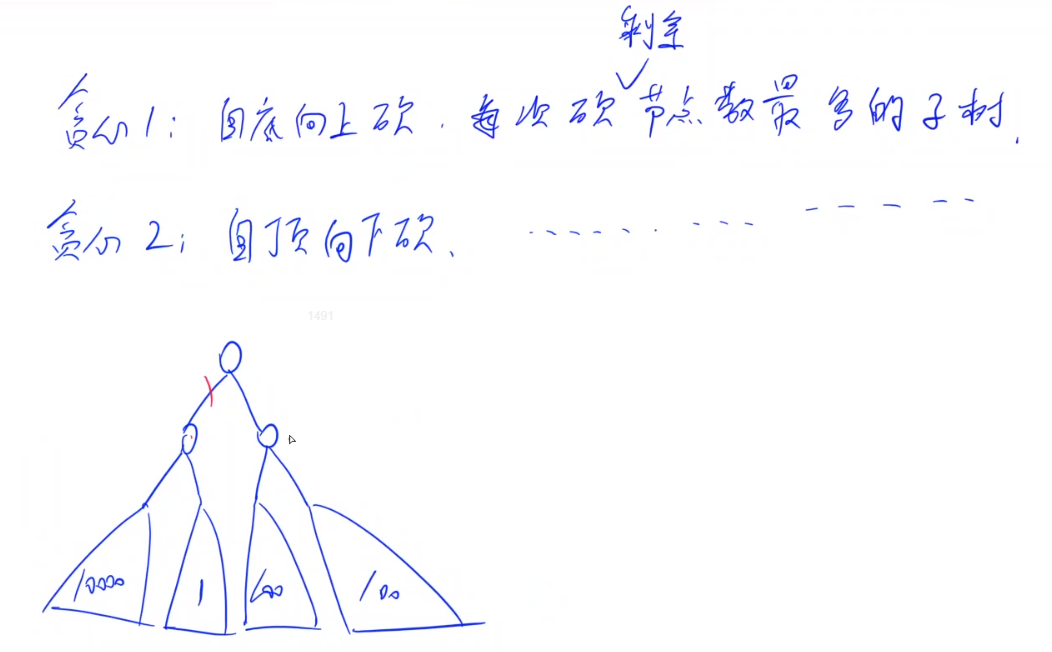
由此,我们排除了贪心做法,然后反观数据范围,发现巨小,所以可以用搜索解法来写,分别枚举每条边来遍历。
算法确定以后,就可以去看一下时间复杂度是否合适,因为n<=30,所以不会超时。时间复杂度分析可看y总题解。
所以我们就得到了搜索的做法。
1.我们需要预处理出每一层分别有多少边,因为每一层只能砍掉一条边,所以需要记录一下。
2.需要标记一下被砍掉的边和不能被砍掉的边,这样会减少计算量。
3.最后之间搜索即可
注意事项
1.在防止反向遍历时的判断y总运用了一个比较优秀的方法if (i != (j ^ 1)) // i不是j的反向边
由于方法过于优秀,我当时写了一个比较浪费空间的写法,开了一个判断数组去写,这里可以学习一下下y总的方法,开数组有点浪费空间,时间上也不知道哪个快。
参考文献
敬请观看y总讲解视频或题解
C++ 代码
#include<bits/stdc++.h>
using namespace std;
int ver[100010],ne[100010],head[100010],bian[100010],vv[100010],f[100010];
vector<int> lev[310];
int tot=0;
int ans=1000000000;
void add(int x,int y)
{
ver[++tot]=y;
ne[tot]=head[x];
head[x]=tot;
}
void find_lev(int x,int death,int fa)
{
bian[x]=1;
for(int i=head[x];i;i=ne[i])
{
int y=ver[i];
if(y==fa)
continue;
find_lev(y,death+1,x);
bian[x]+=bian[y];
lev[death].push_back(i);
vv[i]=x;
}
return ;
}
void biaoji(int tot1,int flag)
{
f[tot1]=flag;
for(int i=head[ver[tot1]];i;i=ne[i])
{
if(vv[tot1]==ver[i])
{
continue;
}
biaoji(i,flag);
}
}
void dfs(int death,int sum)
{
ans=min(ans,sum);
for(int i=0;i<lev[death].size();i++)
{
int y=lev[death][i];
if(!f[y])
{
biaoji(y,1);
dfs(death+1,sum-bian[ver[y]]);
biaoji(y,0);
}
}
return ;
}
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=m;i++)
{
int x,y;
cin>>x>>y;
add(x,y);
add(y,x);
}
find_lev(1,1,0);
dfs(1,n);
cout<<ans;
}

