大家都知道kmp啦，这里就不写题目描述,记录一下上课讲的思路

暴力：

Step1:
S : |----------------------------+------------------|
P : |---------+------|

Step2:
S : |----------------------------+------------------|
P :   |---------+------|

Step3:
S : |----------------------------+------------------|
P :    |---------+------|
...
一步步尝试 直到匹配为止

KMP:

一步步尝试的缺点：之前尝试过的有用无用的信息会被丢失
结论：利用好这些信息，可以将时间复杂度降低

具体有哪些信息？

多言不如一图,上图嘿嘿嘿：

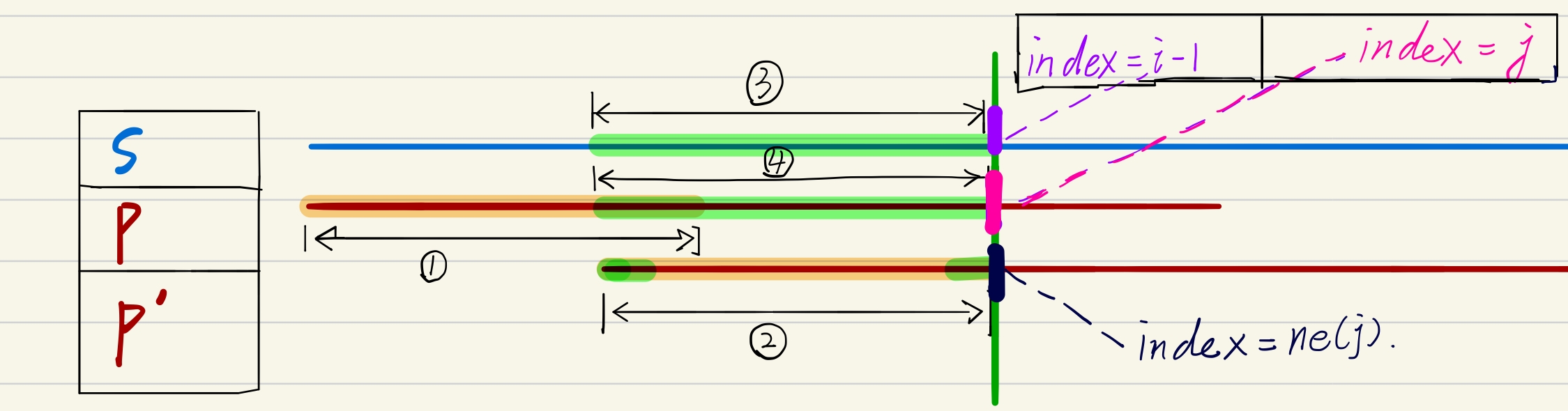
图中 s[3] = p[4] = p'[2] ; p[1] = p'[2] = p[4]
得出：p[1] = p'[2] = p[4];
即：p[1] = p[4](这里的数字表示的是上图中线段的编号，即串中的一段)

这p[1] = p[4]…是什么呢？
暴力解法中一步一步走的过程中一定是从 i不匹配-> i+1不匹配 -> … -> 匹配的过程。十分的漫长啊~
当我们知道p串应该在下一个次移动的时候移动到什么位置时，再也不需要 i,i+1,i+2…进行比较啦，因为$$ p[1] = p[4] $$是“唯一”的，只有当p串起始位置在p[4]的起始位置时才有可能找得到答案.
那么当p[4]越长，我们能跳过的位置就越多，速度也越快，直到p[1]和p[4]出现了交集，由快变慢，但这也会比一步一步走快（或是相同）。

寻找最长的p[4] 求next数组

由于是在p串自身前i位找一个最长的前缀和后缀，满足前缀和后缀相等(next数组)，这对任意一个串都可以找其next数组，假设这个串为str.
为了方便寻找，将str前i位按1 ~ i 注明下标

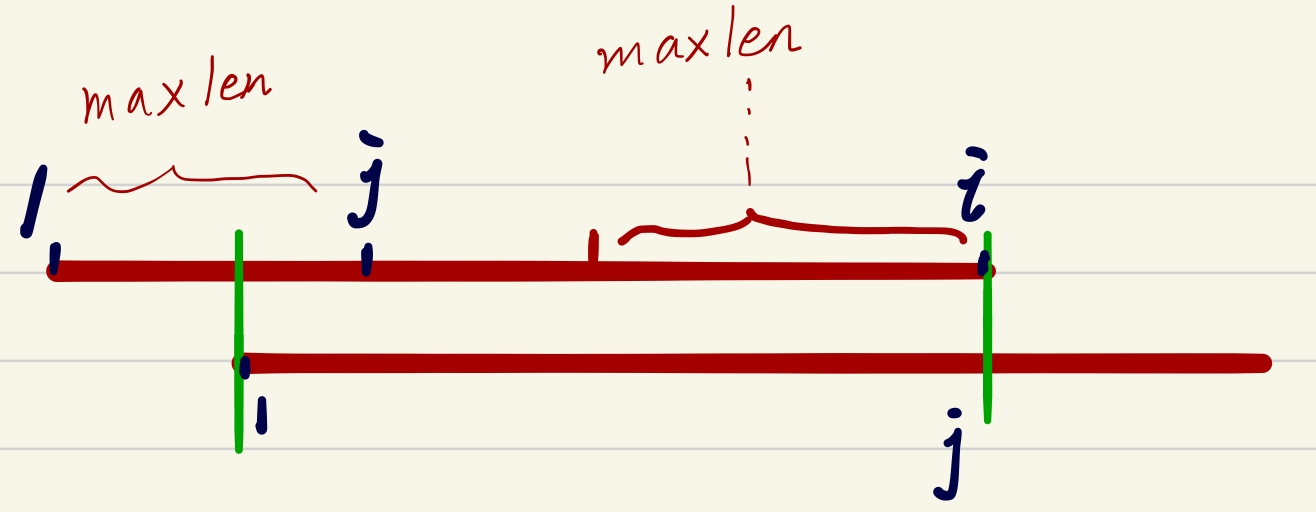
str[i-j+1 ~ i] == str[1~j]:记为nei;

这里的i和j错开一位(起始时i = j-1)
while(str[i] != str[j+1]) j = ne[j];
if(str[i] == str[j+1])i++,j++;
ne[i] = j;

C++ 代码

#include<iostream>
using namespace std;
const int N = 1e5+10,M = 1e6+10;
int n,m,ne[M];
char s[M],p[N];

int main()
{
    cin >> n >> p+1 >> m >> s+1;
    for(int i = 2, j = 0 ; i <= n;i++)
    {
        while(p[i]!= p[j+1] && j) j = ne[j];
        if(p[i] == p[j+1])j++;
        ne[i] = j;
    }
    for(int i = 1,j = 0 ; i <= m;i++)
    {
        while(s[i]!=p[j+1] && j)j = ne[j];
        if(s[i] == p[j+1])j++;
        if(j==n)
        {
            cout << i-n << " ";
            j = ne[j];
        }
    }
    return 0;
}