题目描述

Tom最近在研究一个有趣的排序问题。

通过2个栈S1和S2，Tom希望借助以下4种操作实现将输入序列升序排序。

操作a

如果输入序列不为空，将第一个元素压入栈S1

操作b

如果栈S1不为空，将S1栈顶元素弹出至输出序列

操作c

如果输入序列不为空，将第一个元素压入栈S2

操作d

如果栈S2不为空，将S2栈顶元素弹出至输出序列

如果一个1~n的排列P可以通过一系列操作使得输出序列为1, 2,…,(n-1), n，Tom就称P是一个”可双栈排序排列”。

例如(1, 3, 2, 4)就是一个”可双栈排序序列”，而(2, 3, 4, 1)不是。

下图描述了一个将(1, 3, 2, 4)排序的操作序列：a, c, c, b, a, d, d, b

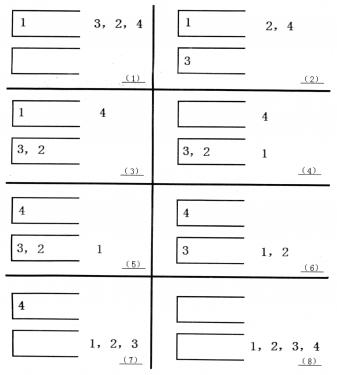
当然，这样的操作序列有可能有几个，对于上例(1, 3, 2, 4)，a, c, c, b, a, d, d, b是另外一个可行的操作序列。

Tom希望知道其中字典序最小的操作序列是什么。

输入格式

第一行是一个整数n。

第二行有n个用空格隔开的正整数，构成一个1-n的排列。

输出格式

输出共一行，如果输入的排列不是”可双栈排序排列”，输出数字0。

否则输出字典序最小的操作序列，每两个操作之间用空格隔开，行尾没有空格。

样例

输入格式
4
1 3 2 4

输出格式
a b a a b b a b

算法1

(染色法，栈) $O(n^2)$

首先还是分析题面，用两个栈对序列进行从小到大排序，并输出最小字典序的操作。

题目大意明确后，就可以思考怎么去做了，我之前是直接模拟去做的，跟秦淮岸大佬做法类似，但是，最近在观看大佬题解的时候发现评论下有个hack数据，所以我还是来学习了一波y总讲解的二分图做法。

首先说一下，怎么与二分图联系起来。

在这里先说一个性质，

(a[k]<a[i]<a[j])&&(i<j<k)

如果满足这个条件的话，那么i和j不能放入到同一个栈当中。
因为a[k]需要在a[i]和a[j]之前被弹出，但是a[k]又需要在a[i]和a[j]之后入栈，显然a[i]不能在a[j]之前出栈，即a[i]和a[j]不能在同一个栈当中。

所以在此就可以利用一下二分图的知识，二分图就是把一堆点分为两堆，且每堆内的点没有连线。

根据这个性质，我们可以把不能在同一个栈当中的元素的下标连一条边，然后进行二分图染色法判断，如果是二分图，说明可以，不是二分图即为无解。

因为要字典序最小，所以尽量插入到第一个栈当中，在此我设染色为1的为第一个栈。

通过染色法分完元素下标后，然后模拟一下即可。

参考文献

敬请观看y总讲解视频或题解

https://www.acwing.com/solution/content/3710/

C++ 代码

#include<bits/stdc++.h>
using namespace std;
int head[100010],ne[100010],ver[100010],a[100010],tot=0,f[100010];
stack<int>st1,st2;
int c[100010];
void add(int x,int y)
{
    ver[++tot]=y;
    ne[tot]=head[x];
    head[x]=tot;
}
bool dfs(int x,int cc)
{
    c[x]=cc;
    for(int i=head[x];i;i=ne[i])
    {
        if(!c[ver[i]]&&!dfs(ver[i],3-cc))
        {
            return 0;
        }
        if(c[ver[i]]==cc)
        {
            return 0;
        }
    }
    return 1;
}
int main()
{
    int n;
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
    }
    f[n+1]=n+1;
    for(int i=n;i>=1;i--)
    {
        f[i]=min(f[i+1],a[i]);
    }
    for(int i=1;i<=n;i++)
    {
        for(int j=i+1;j<=n;j++)
        {
            if(a[i]<a[j]&&a[i]>f[j+1])
            {
                add(i,j);
                add(j,i);
            }
        }
    }
    for(int i=1;i<=n;i++)
    {
        if(!c[i]&&!dfs(i,1))
        {
            puts("0");
            return 0;
        }
    }
    // for(int i=1;i<=n;i++)
    // {
    //     cout<<c[i]<<' ';
    // }
    int t=1;
    for(int i=1;i<=n;i++)
    {
        if(c[i]==1)
        {
            st1.push(a[i]);
            cout<<"a ";
        }
        if(c[i]==2)
        {
            st2.push(a[i]);
            cout<<"c ";
        }
        while(1)
        {
            if(st1.size()&&st1.top()==t)
            {
                st1.pop();
                cout<<"b ";
                t++;
            }
            else if(st2.size()&&st2.top()==t)
            {
                st2.pop();
                cout<<"d ";
                t++;
            }
            else
            break;
        }
    }
}