问题描述

Given a string s, find the longest palindromic subsequence’s length in s. You may assume that the maximum length of s is 1000.

计算出字符串中最长回文子序列。

举个例子：

Example 1:

Input:
"xbcacay"

Output:
5

One possible longest palindromic subsequence is "bcaca".

Update at 2020_0723

总体思路还是不变，简化一下代码：

class Solution {
    public int longestPalindromeSubseq(String s) {

        int n = s.length();
        int[][] dp = new int[n][n];
        int ans = 0;
        for (int i = n - 1; i >= 0; i--){
            dp[i][i] = 1;
            for (int j = i + 1; j < n; j++){
                if (s.charAt(i) == s.charAt(j)){
                    dp[i][j] = dp[i + 1][j - 1] + 2;
                } else {
                    // 挑出左、下的最大值
                    dp[i][j] = Math.max(dp[i][j - 1], dp[i + 1][j]);
                }
            }
        }
        return dp[0][n - 1];
    }
}

解法1

Thanks @tankztc{:target=”_blank”}

先来看下示意图：

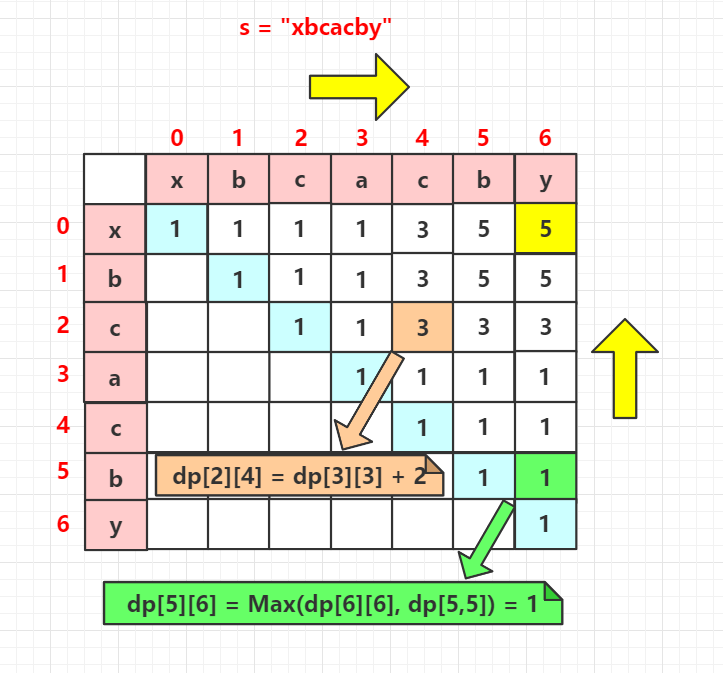
这道题仍使用DP思想，但是有些特别，因为dp[i][j]的计算依赖于下、左、左下三个元素，

因此需要从下往上，从左往右计算，最终的结果取dp[0][len-1]。

同时需要区分两种情况：

如果两个字符相等，那么： dp[i][j] = 左下 + 2

如果两个字符不等，则： dp[i][j] = Max(左、下)

来看下实现：

class Solution {
    public int longestPalindromeSubseq(String s) {
        int len = s.length();
        // Corner case
        if (len == 0) return 0;
        if (len == 1) return 1;
        int[][] dp = new int[len][len];

        /**
         * ------->
         *        ^
         *        |
         *        |
         */
        for (int i = len - 2; i >= 0; i--){
            dp[i][i] = 1;
            for (int j = i + 1; j < len; j++){
                char row = s.charAt(i);
                char col = s.charAt(j);
                if (row == col){
                    dp[i][j] = dp[i + 1][j - 1] + 2;
                } else {
                    dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);
                }
            }
        }

        return dp[0][len - 1];
    }
}

Enjoy it !