题目描述
给定一个整数数组 $nums$,其中恰好有两个元素只出现一次,其余所有元素均出现两次。
样例
输入:[1,2,1,3,2,5]
输出:[3,5]
时间复杂度: 遍历两边$O(2n)=O(n)$ 空间复杂度$O(C)$
算法1
(XOR位运算) $O(n)$
class Solution:
def singleNumber(self, nums: List[int]) -> int:
# XOR算法
xor = 0
a = 0
b = 0
for n in nums:
xor ^= n #位比较 同样则为0 不同则为1
m = 1
#位运算 & 参与运算的两个值,如果两个相应位都为1,则该位的结果为1 反之0
while (xor&m == 0):
m = m << 1
# 即他们!= 0只有一个共有digit来自xor和mask that equals to 1 (xor = 0110, mask = 0010)
for n in nums:
if n&m:
a^= n
else:
b^= n
return [a, b]
人类思维:
n = list(set(nums))
i = 0
j = 0
a = {}
for i in range(len(n)):
if nums.count(n[i]) == 1:
a[j] = n[i]
j += 1
return [a[0], a[1]]
同样也是Explore Card July 24题目
Python位运算整理:
a = 0011 1100
b = 0000 1101
-----------------
a&b = 0000 1100
a|b = 0011 1101
a^b = 0011 0001
~a = 1100 0011
| 运算符 | 描述 | 实例 |
|---|---|---|
| & | 按位与运算符:参与运算的两个值,如果两个相应位都为1,则该位的结果为1,否则为0 | (a & b) 输出结果 12 ,二进制解释: 0000 1100 |
| | | 按位或运算符:只要对应的二个二进位有一个为1时,结果位就为1。 | (a | b) 输出结果 61 ,二进制解释: 0011 1101 |
| ^ | 按位异或运算符:当两对应的二进位相异时,结果为1 | (a ^ b) 输出结果 49 ,二进制解释: 0011 0001 |
| ~ | 按位取反运算符:对数据的每个二进制位取反,即把1变为0,把0变为1 。~x 类似于 -x-1 | (~a ) 输出结果 -61 ,二进制解释: 1100 0011,在一个有符号二进制数的补码形式。 |
| << | 左移动运算符:运算数的各二进位全部左移若干位,由 << 右边的数字指定了移动的位数,高位丢弃,低位补0。 | a << 2 输出结果 240 ,二进制解释: 1111 0000 |
| >> | 右移动运算符:把”>>”左边的运算数的各二进位全部右移若干位,>> 右边的数字指定了移动的位数 | a >> 2 输出结果 15 ,二进制解释: 0000 1111 |
$1 bit$ 情况 即只要$0$ 或者$1$
for (int i : nums) {
xm ^= (xm-1 & ... & x1 & i);
xm-1 ^= (xm-2 & ... & x1 & i);
.....
x1 ^= i;
mask = ~(y1 & y2 & ... & ym) where yj = xj if kj = 1, and yj = ~xj if kj = 0 (j = 1 to m).
xm &= mask;
......
x1 &= mask;
}
II – $32bit$的通例General case with $32-bit$ numbers
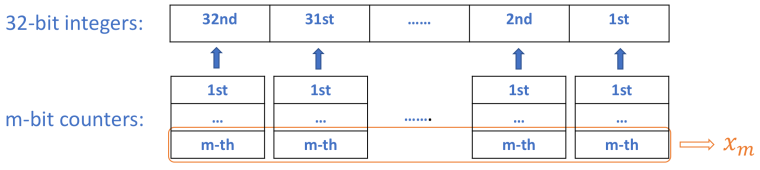
关系 $x_j$和 $p’_j$ 和单个数s : 注:$p’ = p$ % $k$
公式Formula:($x_j)_r$ = $s_r$ & $p’j$
来自fun4LeetCode大佬
样例 Example
$1.~k = 2, p = 1$
只需要32bit里的$x_1$, $2^m = k$ 所以无需mask
public int singleNumber(int[] nums) {
int x1 = 0;
for (int i : nums) {
x1 ^= i;
}
return x1;
}
$2.~k = 3, p = 1$
即$m = 2$ 需要($x_2$, $x_1$), $2^m > k$ –> 加mask = ~($x_1$ & $x_2$)
public int singleNumber(int[] nums) {
int x1 = 0, x2 = 0, mask = 0;
for (int i : nums) {
x2 ^= x1 & i;
x1 ^= i;
mask = ~(x1 & x2);
x2 &= mask;
x1 &= mask;
}
return x1; // Since p = 1, in binary form p = '01', then p1 = 1, so we should return x1.
// If p = 2, in binary form p = '10', then p2 = 1, and we should return x2.
// Or alternatively we can simply return (x1 | x2).
}

