堆排序

• 大根堆：除了叶节点外，每个节点的值都大于等于它的左右儿子
• 小根堆：除了叶节点外，每个节点的值都大于等于它的左右儿子

基本思想（大根堆为例）

• （1）将待排序的序列构造成大根堆，根据大根堆的性质，堆顶就是最大的元素
• （2）将堆顶元素和最后一个元素(叶子节点中最右边的节点）交换，然后将剩下的节点重新构造大根堆，如此反复
• （3）直到只剩一个元素说明已经排好序了

操作

• 建堆

void buildHeap() //建堆
{
    for (int i = cnt/2; i ;i--)
    {
        down(i);
    }
}

为啥从下到上遍历：如果从上往下遍历，当某个节点即是父节点又是子节点并且它的子节点仍然有子节点的时候，因为子节点还没有遍历到，所有子节点不符合大根堆的性质，当子节点调整的时候，必然会影响父节点的二次调整。举个例子：

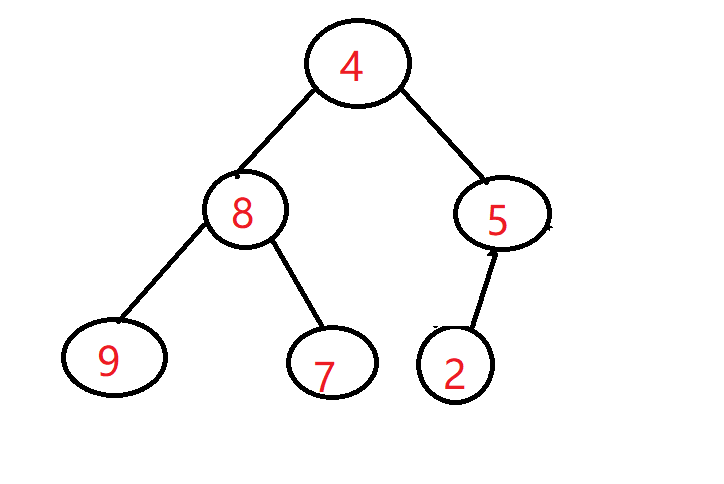
当从上往下遍历时很明显，遍历一次之后根节点是8，而不是9，这就需要二次调整很麻烦，所以从下往上遍历的优势体现出来了

• 调整堆（小根堆）

void down(int u)  //调整堆
{
    //t表示3个节点中的最小值
    int t = u;
    int lchild = 2*u;
    int rchild = 2*u+1;

    if (lchild <= cnt && h[lchild] < h[t]) t = lchild;
    if (rchild <= cnt && h[rchild] < h[t]) t = rchild;
    if (u != t) //不是父节点的值就交换一下
    {
        swap(h[u], h[t]);
        down(t);
    }
}

时间复杂度$ O(nlogn) $，空间复杂度$ O(1) $

C++代码

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
using namespace std;
const int N = 100010;

int n,m;
int h[N],cnt;

void down(int u)  //调整堆
{
    int t = u;
    int lchild = 2*u;
    int rchild = 2*u+1;

    if (lchild <= cnt && h[lchild] < h[t]) t = lchild;
    if (rchild <= cnt && h[rchild] < h[t]) t = rchild;
    if (u != t)
    {
        swap(h[u], h[t]);
        down(t);
    }
}

void buildHeap() //建堆
{
    for (int i = cnt/2; i ;i--)
    {
        down(i);
    }
}

int main ()
{
    scanf("%d%d",&n, &m);
    for (int i = 1; i <= n; i++) scanf("%d",&h[i]);
    cnt = n;

    buildHeap();

    while(m-- )
    {
        printf("%d ",h[1]);
        h[1] = h[cnt--];
        down(1);
    }
    return 0;
}