题目描述

Given the array nums, for each nums[i] find out how many numbers in the array are smaller than it.
That is, for each nums[i] you have to count the number of valid j’s such that j != i and nums[j] < nums[i].

给你一个数组，分别求出小于当前值的总数。

举个例子：

Input: nums = [8,1,2,2,3]
Output: [4,0,1,1,3]
Explanation: 
For nums[0]=8 there exist four smaller numbers than it (1, 2, 2 and 3). 
For nums[1]=1 does not exist any smaller number than it.
For nums[2]=2 there exist one smaller number than it (1). 
For nums[3]=2 there exist one smaller number than it (1). 
For nums[4]=3 there exist three smaller numbers than it (1, 2 and 2).

有如下两个限制：

2 <= nums.length <= 500
0 <= nums[i] <= 100

Update at 2020_0726

这道题还是很有意思的，重新来梳理一下：

先来看下示意图：

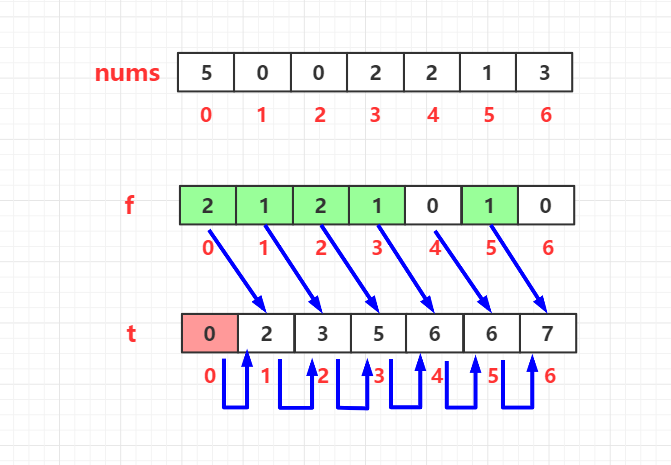
首先，我们遍历原始数组，然后使用数组f统计每个元素出现的次数。

然后，用错位累加法统计小于当前值的数量，并记于数组t中。

最后，再次遍历原始数组，从数组t中获取相应值即可。

时空复杂度均为O(n)

强调两个小细节:

第一，因为0 <= nums[i] <= 100，所以为了便于处理边界问题，直接创建的辅助数组长度为110。

第二，数组t中索引为0时需要特殊处理，赋0即可，在nums[i]范围内，不可能有元素小于0。

再来看下完整实现：

class Solution {
    public int[] smallerNumbersThanCurrent(int[] nums) {

        int N = 110;
        int n = nums.length;
        int[] f = new int[N];
        int[] t = new int[N];
        int[] ans = new int[n];

        // 1. 统计每个元素出现的次数
        for (int i: nums){
            f[i]++;
        }

        // 2. 错位累加
        for (int i = 1; i < N; i++){
            t[i] = t[i - 1] + f[i - 1];
        }
        t[0] = 0;

        // 3. 获取小于当前值的元素的数量。
        for (int i = 0; i < n; i++){
            ans[i] = t[nums[i]];
        }

        return ans;
    }
}