题目描述

给你一个整数数组 bloomDay，以及两个整数 m 和 k 。

现需要制作 m 束花。制作花束时，需要使用花园中 相邻的 k 朵花 。

花园中有 n 朵花，第 i 朵花会在 bloomDay[i] 时盛开，恰好 可以用于 一束 花中。

请你返回从花园中摘 m 束花需要等待的最少的天数。如果不能摘到 m 束花则返回 -1 。

样例1

输入：bloomDay = [1,10,3,10,2], m = 3, k = 1
输出：3
解释：让我们一起观察这三天的花开过程，x 表示花开，而 _ 表示花还未开。
现在需要制作 3 束花，每束只需要 1 朵。
1 天后：[x, _, _, _, _]   // 只能制作 1 束花
2 天后：[x, _, _, _, x]   // 只能制作 2 束花
3 天后：[x, _, x, _, x]   // 可以制作 3 束花，答案为 3

样例2

输入：bloomDay = [1,10,3,10,2], m = 3, k = 2
输出：-1
解释：要制作 3 束花，每束需要 2 朵花，也就是一共需要 6 朵花。而花园中只有 5 朵花，无法满足制作要求，返回 -1 。

样例3

输入：bloomDay = [7,7,7,7,12,7,7], m = 2, k = 3
输出：12
解释：要制作 2 束花，每束需要 3 朵。
花园在 7 天后和 12 天后的情况如下：
7 天后：[x, x, x, x, _, x, x]
可以用前 3 朵盛开的花制作第一束花。但不能使用后 3 朵盛开的花，因为它们不相邻。
12 天后：[x, x, x, x, x, x, x]
显然，我们可以用不同的方式制作两束花。

样例4

输入：bloomDay = [1000000000,1000000000], m = 1, k = 1
输出：1000000000
解释：需要等 1000000000 天才能采到花来制作花束

样例5

输入：bloomDay = [1,10,2,9,3,8,4,7,5,6], m = 4, k = 2
输出：9

限制

• bloomDay.length == n
• 1 <= n <= 10^5
• 1 <= bloomDay[i] <= 10^9
• 1 <= m <= 10^6
• 1 <= k <= n

算法1

(二分) $O(nlogn)$

1. 如果某一朵花第i天盛开，那么第i+1、i+2、… 天都是盛开，所以每一朵花一旦盛开就一直盛开，随着天数增加，盛开的花必定也越多，具有单调性。这是二分的天数的前提。
2. 然后是怎么二分天数：
   1. 先确定边界l, r, 如果存在答案，那答案必定落在[1, 第max天]的区间；如果不存在答案，那肯定是凑不齐m朵花，也就是数组不足m*k长度，因为最次的情况就是达到最后一天去凑m束花
   2. 接着默写二分模板, 考虑check()函数，根据题意，找到第一个大于等于m的那一天, 然后当二分出mid时，考虑第mid天一共能制作多少束花（记为sum）
      1. 如果 sum >= m 则区间可以更新为 [l, mid]
      2. 否则 sum < m 则区间可以更新为 [mid+1, r]

时间复杂度

• 找出开花天数的最大值，时间复杂度为 $O(n)$
• 二分过程
  • 统计某一天能制作多少束花，时间复杂度为 $O(n)$
  • 每次可以缩小一半的区间，时间复杂度为 $O(logn)$
• 故总的时间复杂度为 $O(n + nlogn)$

Go 代码

func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}

func minDays(bs []int, m int, k int) int {
    n := len(bs)
    if m * k > n {
        return -1
    }

    l, r := 1, 1
    for i := 0; i < n; i ++ {
        r = max(r, bs[i])
    }

    for ; l < r ; {
        mid := (l + r) >> 1

        sum := 0
        for i, tmp := 0, 0; i < n; i ++ {
            if bs[i] <= mid {
                tmp ++
            } else {
                tmp = 0
            }

            if tmp >= k {
                sum ++
                tmp = 0
                if sum >= m {
                    break
                }
            }
        }

        if sum >= m {
            r = mid
        } else {
            l = mid + 1
        }
    }

    return r
}

算法2

(动态维护区间) $O(nlogn)$

• 使用2个数组l[], r[] 分别记录某一点所在区间的左右端点；
  > l[i]：表示i所在区间的左端点的下标
  > r[i]：表示i所在区间的右端点的下标
• 区间内维护的是已经盛开的花，盛开的花是根据天数，并且合并区间需要根据下标，因此需要使用pair存储两个属性,天数和下标；由于必定是先开的花会先有区间，就要根据天数排序，按花的盛开顺序来更新合并哪些区间；
  
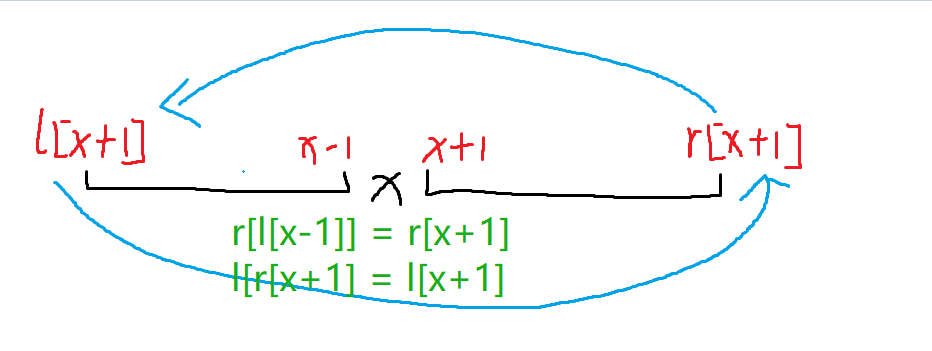
• 当花盛开的时就可以将两段区间合并成一个，合并就相当于改变左右端点的绑定的下标。这里可以分类讨论，比如第x朵花盛开：
  • 当x左右都存在区间时；
  • 当x只有左边的区间时；
  • 当x只有右边的区间时；
  • 当x的左右没有区间时；
• 计算某一段区间内能凑出多少束花，即 区间长度 len / k；其中 len = 右端点-左端点 + 1

时间复杂度

• 排序的时间复杂度是 $O(nlogn)$
• 维护区间左右端点的时间复杂度是 $O(n)$
• 故时间复杂度是 $O(nlogn + n)$

其他

• 类似这题lc.352

Go代码

type pair struct {
    First, Second int
}

func get(l, r, k int) int {
    return (r - l + 1) / k
}

func minDays(bs []int, m int, k int) int {
    n := len(bs)
    p := []pair{}
    l := make([]int, n + 2)
    r := make([]int, n + 2) // n+2容量，实际使用下标是在[1, n],  其中[0]和[n + 1]的边界情况，可以在仅有右区间或仅有左区间时省特判

    for i := 0; i < n; i ++ {
        p = append(p, pair{First : bs[i], Second : i + 1}) // 下标从1开始，
    }

    sort.Slice(p, func(i, j int) bool {
        p1 := p[i]
        p2 := p[j]

        if p1.First != p2.First {
            return p1.First < p2.First
        }
        return p1.Second < p2.Second
    })

    sum := 0
    for i := 0; i < n; i ++ {
        x := p[i].Second

        // 两边都有
        if l[x - 1] > 0 && r[x + 1] > 0 {
            sum = sum - get(l[x - 1], x - 1, k) - get(x + 1, r[x + 1], k) + get(l[x - 1], r[x + 1], k)
            r[l[x - 1]] = r[x + 1]
            l[r[x + 1]] = l[x - 1]

        // 只有左边有
        } else if l[x - 1] > 0 {
            sum = sum - get(l[x - 1], x - 1, k) + get(l[x - 1], x, k)
            r[l[x - 1]] = x
            l[x] = l[x - 1]

        // 只有右边有
        } else if r[x + 1] > 0 {
            sum = sum - get(x + 1, r[x + 1], k) + get(x, r[x + 1], k)
            l[r[x + 1]] = x
            r[x] = r[x + 1]

        // 两边都没有
        } else {
            sum += get(x, x, k)
            l[x] = x
            r[x] = x
        }

        if (sum >= m) {
            return p[i].First
        }
    }

    return -1
}