题目描述

给定二叉树的根节点 root 和一个整数 distance。

如果二叉树中两个 叶 节点之间的 最短路径长度 小于或者等于 distance，那它们就可以构成一组 好叶子节点对。

返回树中 好叶子节点对的数量。

样例

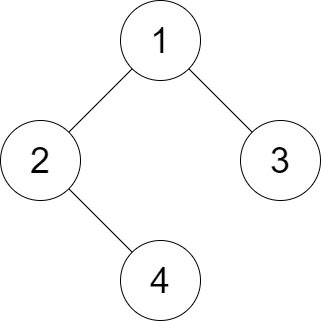
输入：root = [1,2,3,null,4], distance = 3
输出：1
解释：树的叶节点是 3 和 4，它们之间的最短路径的长度是 3。
这是唯一的好叶子节点对。

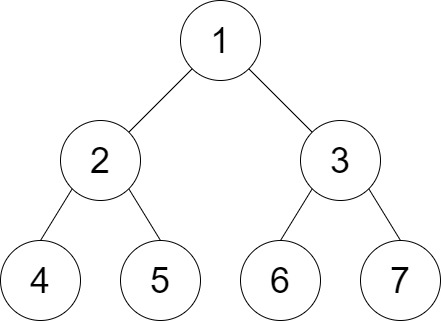
输入：root = [1,2,3,4,5,6,7], distance = 3
输出：2
解释：好叶子节点对为 [4,5] 和 [6,7]，最短路径长度都是 2。
但是叶子节点对 [4,6] 不满足要求，因为它们之间的最短路径长度为 4。

输入：root = [7,1,4,6,null,5,3,null,null,null,null,null,2], distance = 3
输出：1
解释：唯一的好叶子节点对是 [2,5]。

输入：root = [100], distance = 1
输出：0

输入：root = [1,1,1], distance = 2
输出：1

限制

• tree 的节点数在 [1, 2^10] 范围内。
• 每个节点的值都在 [1, 100] 之间。
• 1 <= distance <= 10

算法1

(递归遍历) $O(nh)$

1. 对整棵树进行递归遍历，遍历过程中，记录以当前节点为根节点时，所有叶子节点到当前非叶子节点的路径长度，将这些长度以升序排列，称作长度序列。
2. 对于当前非叶子节点，我们可以获得左右子节点的长度序列 $l$ 和 $r$，此时可以用双指针，在线性时间内统计出符合要求的节点对数。具体地，我们可以对 $l$ 中的每个位置，都求出 $r$ 最大的位置 $j$，满足 $l(i) + r(j) + 2 \le distance$。注意到 $j$ 是单调递减的。
3. 最后，应用归并算法，将左右子节点的长度序列按升序归并。归并时需要将所有的路径长度都加 1。

时间复杂度

• 在每一层最多遍历一次所有叶子节点，设最多有 $h$ 层，时间复杂度为 $O(nh)$。

空间复杂度

• 需要 $O(nh)$ 的额外空间存储递归系统栈和长度序列。

C++ 代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
private:
    int ans;

    void solve(TreeNode *rt, vector<int> &d, int distance) {
        if (!rt) return;

        if (!rt->left && !rt->right) {
            d.push_back(0);
            return;
        }

        vector<int> l, r;

        solve(rt->left, l, distance);
        solve(rt->right, r, distance);

        for (int i = 0, j = r.size() - 1; i < l.size(); i++) {

            // 这里加 2 是因为左右子节点到当前节点的距离为 1。
            while (j >= 0 && l[i] + r[j] + 2 > distance)
                j--;
            ans += j + 1;
        }

        int i = 0, j = 0;
        while (i < l.size() || j < r.size()) {
            if (j == r.size()) {
                d.push_back(l[i] + 1);
                i++;
            } else if (i == l.size()) {
                d.push_back(r[j] + 1);
                j++;
            } else {
                if (l[i] <= r[j]) {
                    d.push_back(l[i] + 1);
                    i++;
                } else {
                    d.push_back(r[j] + 1);
                    j++;
                }
            }
        }
    }

public:
    int countPairs(TreeNode* root, int distance) {
        ans = 0;
        vector<int> d;
        solve(root, d, distance);
        return ans;
    }
};

算法2

(递归遍历) $O(n \cdot distance)$

1. 和算法 1 类似，由于距离最大只有 10，所以我们可以在递归过程中，记录属于每个长度的叶子节点个数有多少个，相当于一个哈希数组。
2. 对当前非叶子节点统计的时候，求出右子节点哈希数组的前缀和。枚举左子节点的距离，将左子节点对应值乘以前缀和数组的对应值，累加答案。

时间复杂度

• 每个非叶子节点只需要 $O(distance)$ 的时间，故总时间复杂度为 $O(n \cdot distance)$。

空间复杂度

• 需要 $O(n \cdot distance)$ 的额外空间存储递归系统栈和哈希数组。

C++ 代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
private:
    int ans;

    void solve(TreeNode *rt, vector<int> &seen, int distance) {
        if (!rt) return;

        if (!rt->left && !rt->right) {
            seen[0]++;
            return;
        }

        vector<int> l(distance), r(distance);

        solve(rt->left, l, distance);
        solve(rt->right, r, distance);

        vector<int> sr(distance);

        sr[0] = r[0];
        for (int i = 1; i < distance; i++)
            sr[i] = sr[i - 1] + r[i];

        for (int i = 0; i < distance - 1; i++)
            ans += l[i] * sr[distance - i - 2];

        for (int i = 1; i < distance; i++)
            seen[i] = l[i - 1] + r[i - 1];
    }

public:
    int countPairs(TreeNode* root, int distance) {
        ans = 0;
        vector<int> seen(distance);
        solve(root, seen, distance);
        return ans;
    }
};