鄙人不才,此中鄙陋甚多,望海涵!!!
类Floyd算法+qmi(快速幂)
时间复杂度 $O(logN*n^3)$ N指的是题中所说从起点S到终点E所经过的边数
//需要在快速幂的框架下做logN次类floyd算法
在研究此题前我们先对比一下类Floyd算法和Floyd算法的区别与联系
普通Floyd
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
d[i][j]=min(d[i][j],d[i][k]+d[k][j]);
我们不难发现之所以Floyd可以得到所有点对间的最短距离是因为每次都是一条边一条边的的更新,图示如下
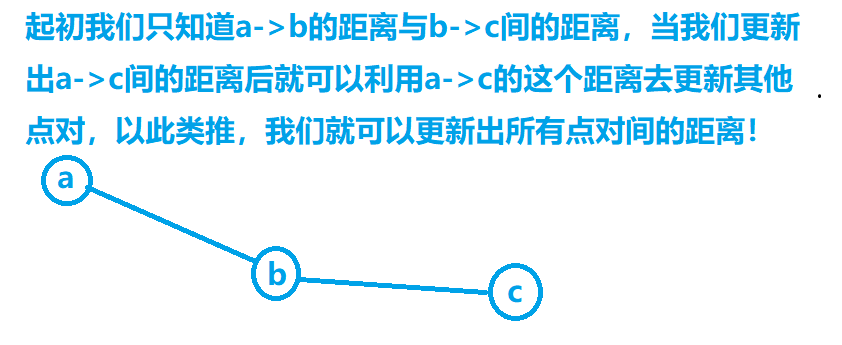
类Floyd算法
static int temp[N][N];
memset(temp,0x3f,sizeof temp);
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
temp[i][j]=min(temp[i][j],a[i][k]+b[k][j]);
我们发现做一次类Floyd好像不用并不会去用该次的结果自我更新,只会用上一次的结果来更新一次,不像Floyd那样可以自己更新自己多次!图示如下
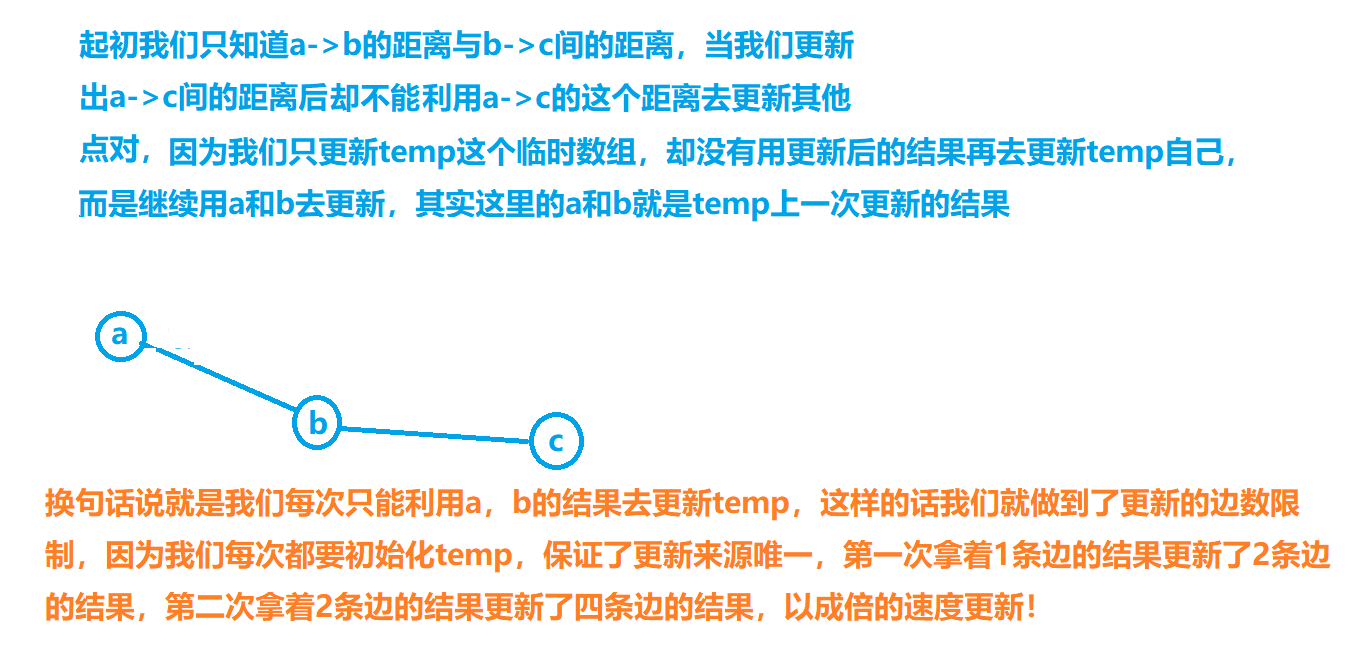
知道了区别后应该就不难理解为什么类Floyd的算法具有了边数的特性了
C++ 代码
#include<iostream>
#include<cstring>
#include<map>
using namespace std;
const int N=210;
int res[N][N],g[N][N];
int k,n,m,S,E;
map<int,int> id;
void mul(int c[][N],int a[][N],int b[][N])
{
static int temp[N][N];
memset(temp,0x3f,sizeof temp);
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
temp[i][j]=min(temp[i][j],a[i][k]+b[k][j]);
memcpy(c,temp,sizeof temp);
}
void qmi()
{
memset(res,0x3f,sizeof res);
for(int i=1;i<=n;i++) res[i][i]=0;//经过0条边
while(k)//更新的过程
{
if(k&1) mul(res,res,g);//res=res*g;根据k决定是否用当前g的结果去更新res
mul(g,g,g);//g=g*g;g的更新
k>>=1;
}
}
int main()
{
cin>>k>>m>>S>>E;//虽然点数较多,但由于边数少,所以我们实际用到的点数也很少,可以使用map来离散化来赋予
//他们唯一的编号
memset(g,0x3f,sizeof g);
//这里我们来解释一下为什么不去初始化g[i][i]=0呢?
//我们都知道在类Floyd算法中有严格的边数限制,如果出现了i->j->i的情况其实在i->i中我们是有2条边的
//要是我们初始化g[i][i]=0,那样就没边了,影响了类Floyd算法的边数限制!
if(!id.count(S)) id[S]=++n;
if(!id.count(E)) id[E]=++n;
S=id[S],E=id[E];
while(m--)
{
int a,b,c;
scanf("%d%d%d",&c,&a,&b);
if(!id.count(a)) id[a]=++n;
if(!id.count(b)) id[b]=++n;
a=id[a],b=id[b];
g[a][b]=g[b][a]=min(g[a][b],c);
}
qmi();
cout<< res[S][E] <<endl;
return 0;
}


我觉得可以这么想,g[i][j]初始代表的是经过1条边,i到j经过的简单路径长度,由于i到i一步走不到,所以为无穷大。而res[i][j]代表的是经过0条边的路径长度,因为他需要和g乘,所以res代表的应该是幺元,也就是单位元,所以他就是经过0条边的路径长度,那么i经过0条边只能到自身,其他点都到不了,到不了的设为无穷。
同样的,temp也是幺元
我在这里稍微给大佬的评论做个解释:
进入快速幂的一开始,res数组存储经过0条边的路径长度。
根据代数结构知识,单位元e的定义: e * a = a,( * 是广义矩阵乘法,满足结合律, a为任意元素),在这道最短路的情境下,就是经过0条边的路径,在经过a条边的路径后,总的路径长度为a,满足单位元的性质。而要满足单位元的性质,就必须要使得 res[i][i] = 0, res[i][j] = 0x3f3f3f3f.
但在求快速幂的时候,res被重新利用或者说是一开始就初始化为单位元是保证答案正确的必要条件,因此res可以最后存储经过k条边的最短路径长度。
但,我和大佬意见不一样的是:temp并不是幺元,因为它并不满足单位元的性质。而temp的作用仅仅就是临时存储 a[i][k]+b[k][j] 的最小值,避免内存报错,不使用temp会导致地址无法被访问,就是y总debug遇到的问题。其实可以把 temp 这个静态变量定义提到外面,变成全局变量,然后每一次进入函数,都会被初始化为0x3f3f3f3f,测试结果是正确的。
鄙人才学浅陋,欢迎大佬指正!
有个问题为什么能倍增?我想的是两个点间4条边的最短距离不应该只是由两条边的最短距离更新啊,可能还有一条边和三条边的情况啊。
是因为这里是个图,最终两两条边组成的最小值一定对应了某个具体的情况,也就是一条经过几个点的具体路线。那么在这个最优线路中(先走两条边再走两条边)和(先走一条边再走三条边)是一样的。这时两条边两条边更新出来的四条边的最小值一定等于一条边和三条边更新出来的四条边的最小值。因为他们最终对应的一定是某个现实的状态。
不知道这样想对不对。
快速幂,类似于可以用二进制拼凑出每一个数
orz orz
好哎
搞懂了
大佬,请问这里最大值为什么设置为0x3f呀,最大路径应该大于这个值呀。
一般题目数据不会比1e9大,这里0x3f比1e9大且只大一点,还能保证2个这样的0x3f相加不会爆int,算是个经验值。
这个做法可以处理负权边吗
佬,
qmi()中的这句注释:if(k&1) mul(res,res,g);//res=res*g;根据k决定是否用当前g的结果去更新res是否改成
res = res + g更合适呢,既然g是表示二进制下的长度,要构成最后答案应该是累加吧%%%
%%%
神!
$tql$
tql, %%%%%%%%%%%%
up主太通俗易懂了
哈哈哈,当时自己也理解了好久,想着别人也有困惑,就写个题解
这种其实就是二进制优化吗
是,qmi就是quick 幂
那个最外层的循环到底是边还是点啊?
之前也觉得是边,但是在dp里面就是d[i][j]=min(d[i][k]+d[k][j])时候感觉就不像边了
其实是点。
边的个数隐含在快速幂中,边的个数是快速幂倍增后的个数。
话说这不就是bellmanford吗
bellmanford是最多 这里是恰好
%%%
明白了,又好像没明白
可以休息休息再看,一直看容易晕
好像搞明白了,每次做Floyd的时候,第一次是经过一条边,第二次是经过两条边,第三次是经过四条边,以此类推。
是
怎么样确定它是有结合律,可以用快速幂的写法。
是不是可以用矩乘理解这个具有结合律
好像听明白了⊙ω⊙
哈哈哈