hash
思想
把比较大的值域映射到一个比较小的空间0 - N, N = (1e5 ~ 1e6)
- 时间复杂度 $\Theta(1)$
存储结构
hash函数一般是取模 : $h(x) = x \% 10^5$ $h(x) \subset [0, 10^5 - 1)$,
取模的数一般取成质数,而且这个质数要离2的整数次幂要远 这样能尽量减少冲突。
一般数学概念里面余数一定是整数,但是在c++里面 $负数\%正数 = 负数$,所以取模的时候一定要把余数转换成正数。
根据处理冲突的方式分为两种存储结构 :
1. 开放寻址法
2. 拉链法
// 求大于100000的第一个质数
for(int i = 100000; ; i ++){
bool flag = true;
for(int j = 2; j * j <= i; j ++){
if(i % j == 0){
flag = false;
break;
}
}
if(flag){
cout << i;
break;
}
}
开放寻址法
- 开放寻址法的数组要开到题目要求的输入数量的两到三倍那么长(降低冲突 sssss概率)
- 插入:从k坑位开始,找空的坑位
- 查找:从k坑位开始找,找到的话就存在,如果遇到一个坑位没有人,那就代表x不存在
- 删除:跟拉链法一样。
INT_MAX是ffffffff。一般比赛喜欢用3f3f3f3f是因为它大于1e9,并且乘以2后依然不会溢出。
#include <iostream>
#include <cstring>
using namespace std;
const int N = 2e5 + 3;
int n, null = 0x3f3f3f3f;
int hmap[N];
int find(int x){
int k = (x % N + N) % N;
while(hmap[k] != null && hmap[k] != x) {
k ++;
if(k == N) k = 0; // 如果找到末尾了那就回到0继续找,循环找
}
return k;
// 返回k有两种可能 1、没找到即hmap[k] != null; 2、找到了,即hmap[k] == x
}
int main(){
cin >> n;
char op[2];
int x, k;
memset(hmap, 0x3f, sizeof hmap); // 按字节来覆盖内存
while(n--){
scanf("%s%d", op, &x);
k = find(x);
if(op[0] == 'I') {
hmap[k] = x;
} else {
if(hmap[k] == x) puts("Yes");
else puts("No");
}
}
return 0;
}
拉链法
- 开一个一维数组来存储哈希值,在对应的哈希值下拉一条链,存储哈希值相等的数。
- 插入:一定能插入,冲突就进链表
- 查找:链表迭代
- 一般情况下不会有删除操作,如果真的需要删除操作,开一个布尔变量的数组,标记需要删除的节点,并不会真的去删除他。
#include <iostream>
#include <cstring>
using namespace std;
const int N = 100003;
int n;
// hmap[]:相当于槽位,存的是链表第一个节点的位置
// e[]:链表节点的值
// ne[]:链表节点的下一个节点的位置
// idx: 当前用到第几个位置
// 链表节点的尾部: ne[idx] = -1
int hmap[N], e[N], ne[N], idx;
void insert(int x){
int k = (x % N + N) % N; // 保证余数是正的
e[idx] = x;
ne[idx] = hmap[k];
hmap[k] = idx ++;
}
bool query(int x){
int k = (x % N + N) % N; // 保证余数是正的
for(int i = hmap[k]; i != -1; i = ne[i]){ // 槽位不空的话
if(e[i] == x) return true;
}
return false;
}
int main(){
cin >> n;
char op[2];
int x;
idx = 0;
memset(hmap, -1, sizeof hmap); // 空槽位设成-1
while(n --){
scanf("%s",op);
if(op[0] == 'I'){
scanf("%d", &x);
insert(x);
}else{
cin >> x;
if(query(x)) puts("Yes");
else puts("No");
}
}
return 0;
}
字符串哈希方式——字符串前缀哈希法
- 先预处理出所有前缀的哈希值
- 可以利用求得的哈希求得任意一个子串的哈希值。
怎么定义字符串的哈希值呢?
将一个字符串看成一个p进制的数,例如一个字符串(假设字符串的字母集位大写字母) A B C D hash值为p进制的 $(1 2 3 4)_p$。
那么他的十进制hash值为 $1 * p^3 + 2 * p^2 + 3 * p^1 + 4 * p^0$。那么通过这样一种方式可以把字符串转化成数字。由于这个数最后可能比较大,位数比较多,可以对其模上一个Q。
即 $(1 * p^3 + 2 * p^2 + 3 * p^1 + 4 * p^0) \% Q$,这样就可以将一个前缀字符串映射到 [0 ~ Q-1] 这个空间里。
注意
1. 不能把某一个字母映射成数字0,例如若将 $A \rightarrow 0$ 那么A的十进制数就是0, AA的十进制数也是0, AAAAAA···的十进制数都是0,这样的话很多字符的哈希值都一样了。
2. 假定人品足够好,不存在冲突(不考虑冲突)。经验: 当p = 131 || p = 13331的时候 $Q = 2^{64}$, 假定不会出现冲突。
如何利用前缀哈希值求任意一个子串的哈希呢?
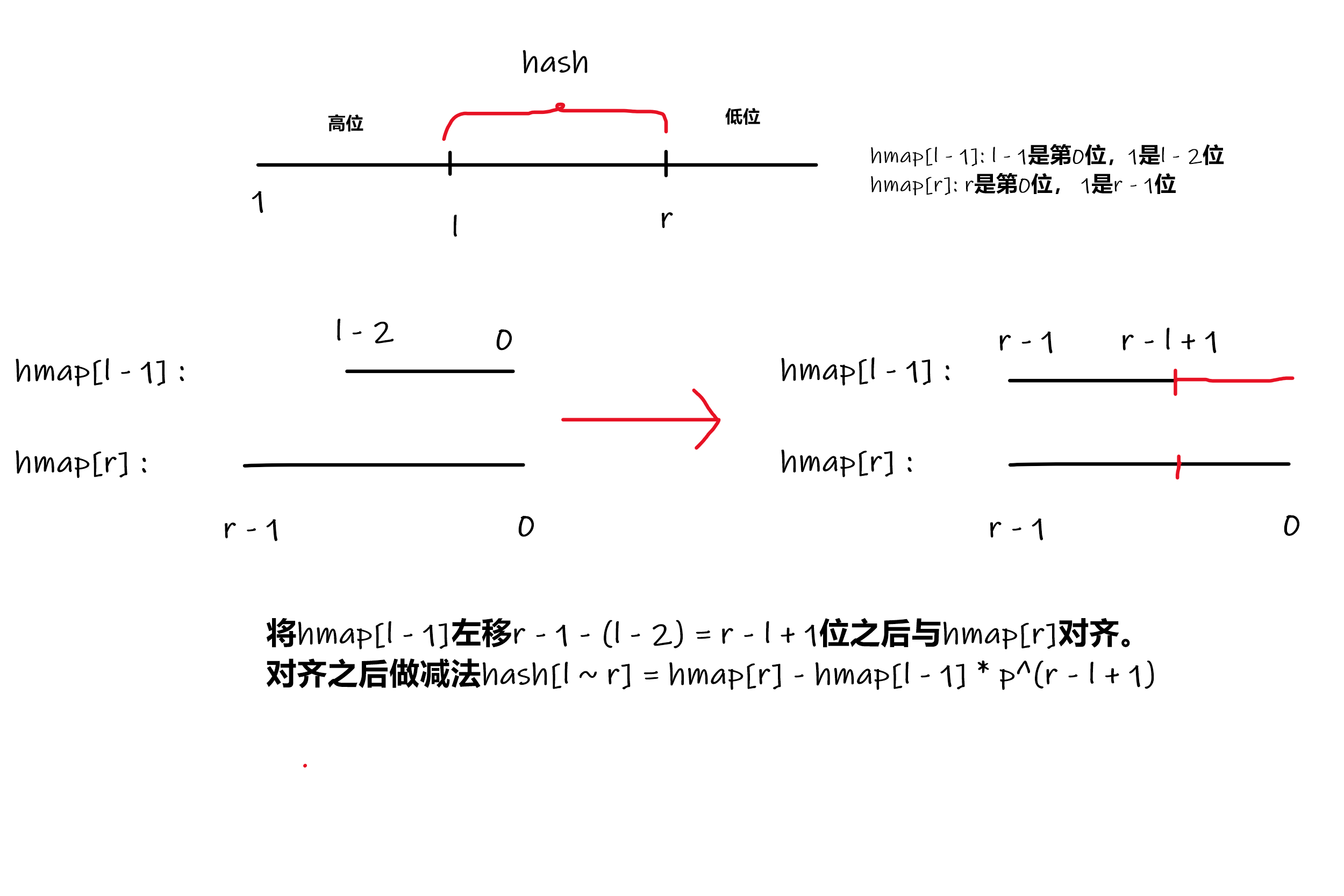
首先将hmap[l - 1] 左移一定的位数让其与hmap[r]对齐,然后做减法。
- 例:将十进制数1234左移3位的做法是 $1234 * 10^3 = 1234000$,那么对于p进制数,左移n位的做法应该是乘上一个$p^n$
- 本来得到的$hmap[r \rightarrow l]$要取模Q,可以用unsign long long来存储这个结果,溢出的部分就相当于取模运算。
- hmap可以这样计算: $hmap[i] = hmap[i - 1] * p + str[i]$ 实际上就是左移,把字符加到最低位。
将hmap[l - 1]左移$p^{r - l + 1}$位,就是乘上$p^{r - l + 1}$,对齐然后做减法
$$ hmap[r \rightarrow l] = hmap[r] - hmap[l - 1] * p^{r - l + 1}$$
#include <iostream>
using namespace std;
typedef unsigned long long ULL;
const int N = 100010, P = 131; // P进制
// p[i]存储p的i次方
// hmap[i]存储前i个字母组成的字符串的哈希值
int n, m;
char str[N];
ULL p[N], hmap[N];
ULL get(int l, int r){
return hmap[r] - hmap[l - 1] * p[r - l + 1];
}
int main(){
scanf("%d%d%s", &n, &m, str + 1); // 从1开始存储
p[0] = 1; // 规定任何数的0次方 = 1
for(int i = 1; i <= n; i++){
p[i] = p[i - 1] * P;
hmap[i] = hmap[i - 1] * P + str[i]; // 字符串前缀的哈希值
}
int l1, r1, l2 ,r2;
while(m --){
scanf("%d%d%d%d", &l1, &r1, &l2, &r2);
if(get(l1, r1) == get(l2, r2)) puts("Yes");
else puts("No");
}
return 0;
}


牛逼