题目描述

根据一棵树的中序遍历与后序遍历构造二叉树。

注意:
你可以假设树中没有重复的元素。

样例

例如，给出

中序遍历 inorder = [9,3,15,20,7]
后序遍历 postorder = [9,15,7,20,3]

返回如下的二叉树：

    3
   / \
  9  20
    /  \
   15   7

算法分析

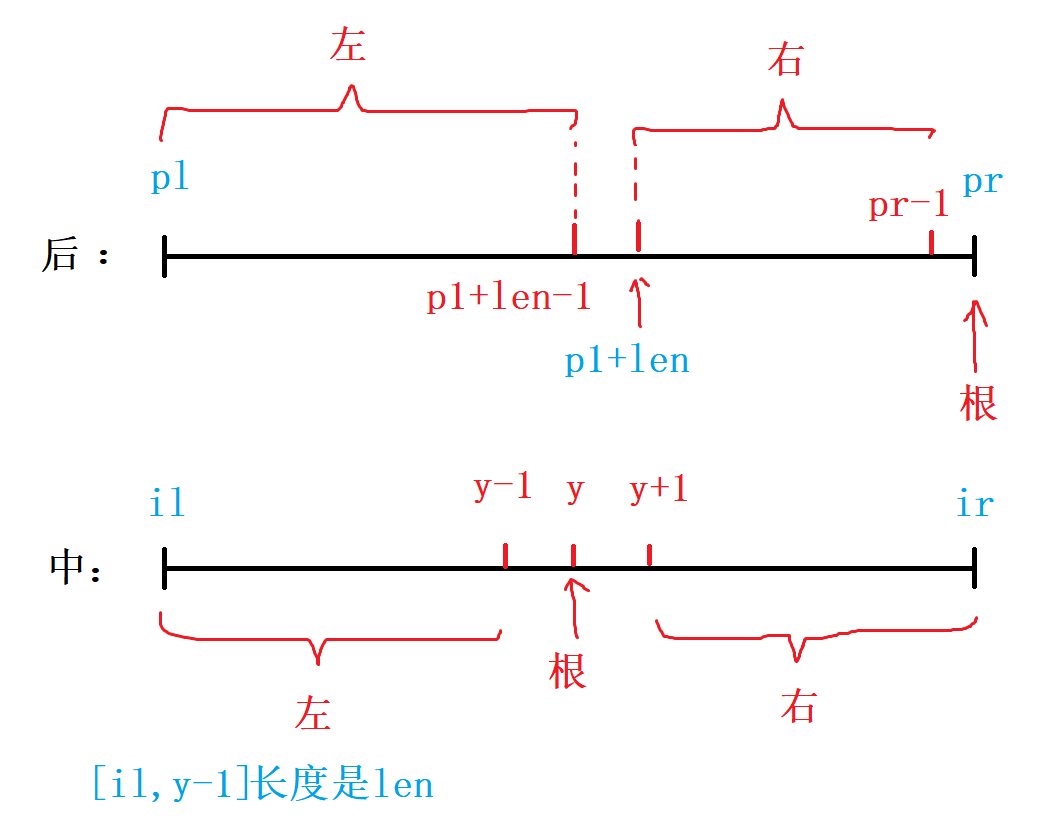
如图所示，[pl,pr]和[il,ir]分别以后序和中序的方式维护一棵树，后序遍历的最后一个元素则是当前树的根结点的值x，找到x值在中序遍历的位置y，可知[pl,pl + len - 1]和[il,y - 1]维护的是同一棵左子树，[pl + len,pr - 1]和[y + 1,ir]维护的是同一颗右子树

时间复杂度 $O(n)$

Java 代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    static Map<Integer,Integer> map = new HashMap<Integer,Integer>();
    static TreeNode build(int[] postorder, int[] inorder, int pl, int pr, int il, int ir)
    {
        if(pl > pr || il > ir) return null;
        int x = postorder[pr];
        int y = map.get(x);
        int len = y - il;
        TreeNode root = new TreeNode(x);
        root.left = build(postorder, inorder, pl, pl + len - 1, il, y - 1);
        root.right = build(postorder, inorder, pl + len, pr - 1, y + 1, ir);
        return root;
    }
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        map.clear();
        int n = inorder.length;
        for(int i = 0;i < n;i ++)
        {
            map.put(inorder[i], i);
        }
        return build(postorder, inorder, 0, n - 1, 0, n - 1);
    }
}