题目描述

给定一个正整数 n，将其拆分为至少两个正整数的和，并使这些整数的乘积最大化。 返回你可以获得的最大乘积。

样例

算法1

时间复杂度 $O(0)$ 神速 没有更快 除非你是神

C++ 代码

int integerBreak(int n) {
    return (vector<int>{ -1, -1, 1, 2, 4, 6, 9, 12, 18, 27, 36, 54, 81, 108, 162, 243, 324, 486, 729, 972, 1458, 2187, 2916, 4374, 6561, 8748, 13122, 19683, 26244, 39366, 59049, 78732, 118098, 177147, 236196, 354294, 531441, 708588, 1062882, 1594323, 2125764, 3188646, 4782969, 6377292, 9565938, 14348907, 19131876, 28697814, 43046721, 57395628, 86093442, 129140163, 172186884, 258280326, 387420489, 516560652, 774840978, 1162261467, 1549681956  })[n];
}

算法2

(还是数学方法好) $O(1)$

数学方法，求函数$y=(n/x)^x(x>0)$的最大值，可得x=e时y最大，但只能分解成整数，故x取2或3，由于6=2+2+2=3+3，显然2^3=8<9=3^2,故应分解为多个3

Python 代码

class Solution:
    def integerBreak(self, n: int) -> int:
        if(n == 2): return 1
        if(n == 3): return 2
        a = 1
        while(n > 4):
            n = n - 3
            a = a * 3
        return a * n

算法3 DP
状态转移方程如下：
$dp[i]= \max_{1<=j<i}{max(j×(i−j),j×dp[i−j])\}$
$dp[i]= \max_{1<=j<i}$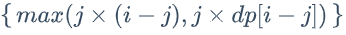
$$ \left\{ \begin{array} {rcl}{max(j×(i−j),j×dp[i−j])} \end{array}\} \right. 不知道为啥不能正确显示{}，cnBlog里的引擎和本地markdown(Typora的LaTeX)却可以 $$

$当i>3$时$dp[i]=max(2×(i−2),2×dp[i−2],3×(i−3),3×dp[i−3])$

class Solution:
    def integerBreak(self, n: int) -> int:
        if n < 4:
            return n - 1

        dp = [0] * (n + 1)
        dp[2] = 1
        for i in range(3, n + 1):
            dp[i] = max(2 * (i - 2), 2 * dp[i - 2], 3 * (i - 3), 3 * dp[i - 3])

        return dp[n]