题目描述

给定一个非负索引 k，其中 k ≤ 33，返回杨辉三角的第 k 行。

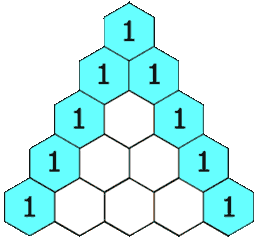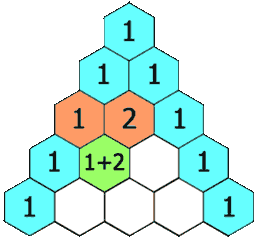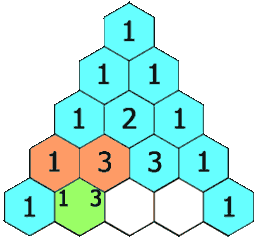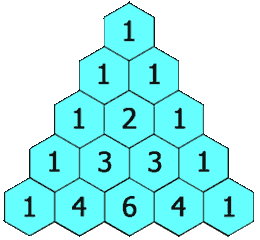
在杨辉三角中，每个数是它左上方和右上方的数的和。

样例

输入: 3
输出: [1,3,3,1]

进阶：

你可以优化你的算法到 O(k) 空间复杂度吗？

算法分析

组合数

• 1、对于杨辉三角形来说，每一行的元素都是$(x + 1)^k$的展开式的对应的系数，从第0行开始计算
• 2、对于第k行，一共有k + 1个元素，分别对应的是$C_k^0$，$C_k^1$，$C_k^2$ … $C_k^k$
• 3、给定k时，可以直接通过公式计算出第k行的所有元素

时间复杂度 $O(n)$

空间复杂度 $O(n)$

Java 代码

class Solution {
    public List<Integer> getRow(int n) {
        int[] C = new int[n + 10];

        int k = n;
        int t = 1;
        long res = 1;
        for(int i = 0;i <= n;i ++)
        {
            C[i] = (int)res ;
            res = res * (k --) / (t ++);
        }

        List<Integer> ans = new ArrayList<Integer>();
        for(int i = 0;i <= n;i ++)
        {
            ans.add(C[i]);
        }
        return ans;
    }
}