题目描述

给定一个三角形，找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。

相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。

样例

例如，给定三角形：

[
     [2],
    [3,4],
   [6,5,7],
  [4,1,8,3]
]

自顶向下的最小路径和为 11（即，2 + 3 + 5 + 1 = 11）。

说明：

如果你可以只使用 O(n) 的额外空间（n 为三角形的总行数）来解决这个问题，那么你的算法会很加分。

算法分析

自顶向下的解法

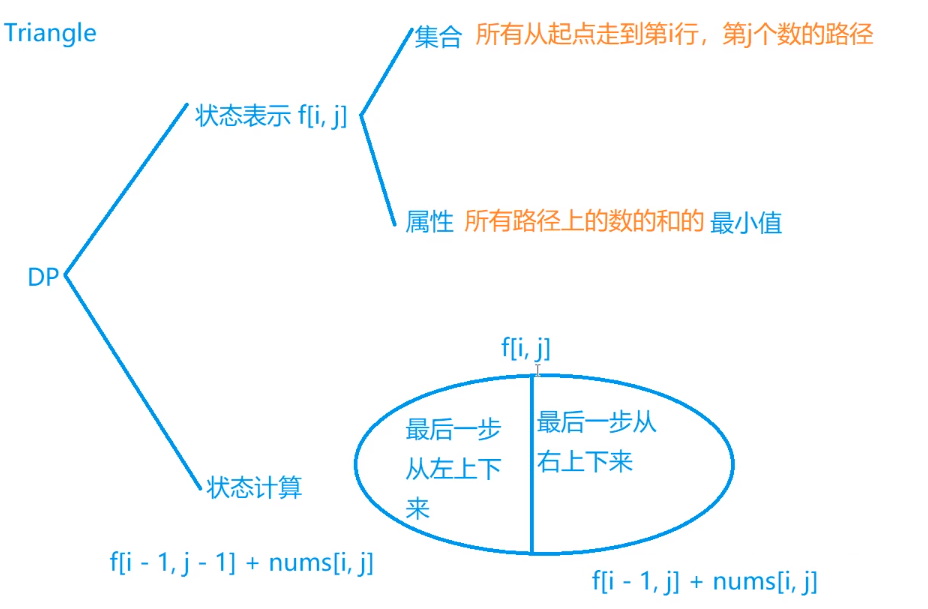
还可以用自底向上的解法，比自顶向下还快

时间复杂度 $O(n^2)$

空间复杂度 $O(1)$

原地修改

Java 代码

class Solution {
    public int minimumTotal(List<List<Integer>> triangle) {
        int n = triangle.size();
        for(int i = 1;i < n;i ++)
        {
            for(int j = 0;j <= i;j ++)
            {   
                int t = 0x3f3f3f3f;
                if(j - 1 >= 0) t = Math.min(t, triangle.get(i - 1).get(j - 1));
                if(j < i) t = Math.min(t, triangle.get(i - 1).get(j));
                int val = triangle.get(i).get(j);
                triangle.get(i).set(j,val + t);
            }
        }
        int ans = 0x3f3f3f3f;
        for(int i = 0;i < n;i ++) ans = Math.min(ans, triangle.get(n - 1).get(i));
        return ans;
    }
}