题目描述

题目里有一堆麻烦的输入，还有让人头疼的各种变量，但还是逃不过模拟题的本质——依据题目描述用程序实现功能+细节优化=Accepted

很明显，模拟题就是管你看没看懂，模拟就完了！

题目大概说了这样一件事，有 $m$ 台机器，$n$ 个工件，每个工件 $m$ 道工序，每道工序都由 指定 的不同的机器完成,每道工序时间都不同，然后求最快多长时间加工完毕。
于是题目分别给了“$m,n$，指定顺序，每个工件的每个工序分配给的机器和每个工件的每个工序分配给的时间”这些条件

样例

【输入】

2 3
1 1 2 3 3 2
1 2 
1 2 
2 1
3 2 
2 5 
2 4

【输出】

10

(算法：%你)

到此为止，我们掌握了几乎所有的数据，然后我们可以开始思考，既然要时间最短，又要全部完成，而且还是已指定顺序，所以按照给定的工作顺序判断哪台机器可以使用，见缝插针就可以了。
所以我们第一重循环是遍历工作顺序
工作的信息里提到了工作时间和工作的机器，所以我们不需要遍历所有机器，直接指定题目给定的目标机器
然后我们遍历时间轴，寻找这台机器什么时候有时间，为了节约时间，找到距离开始时间最近的解就是最优解，同时作为工作时间的一段时间轴上不能有一点被占用的。
当我们找到这样的一段时间轴时，将需要占用的时间轴全部用工程师占了，这样的话就需要知道是从是么时候开始占用的。
我们可以用超时空转换将工程师传送到开始的位置
另外，请无视下面的这行字，这不是广告！！！

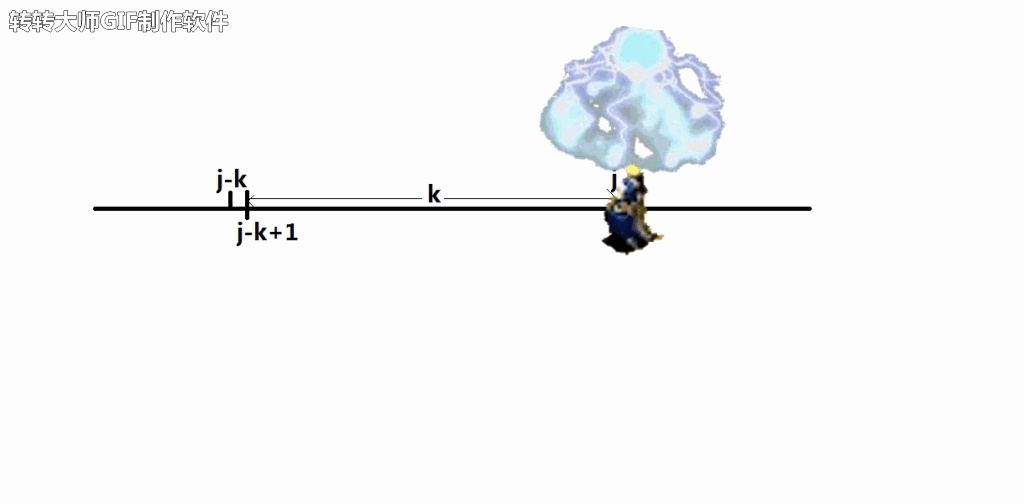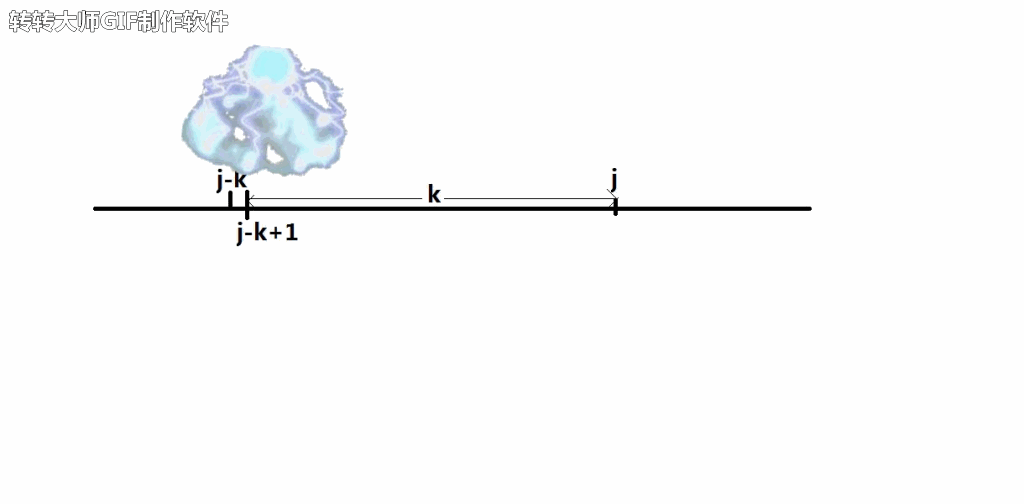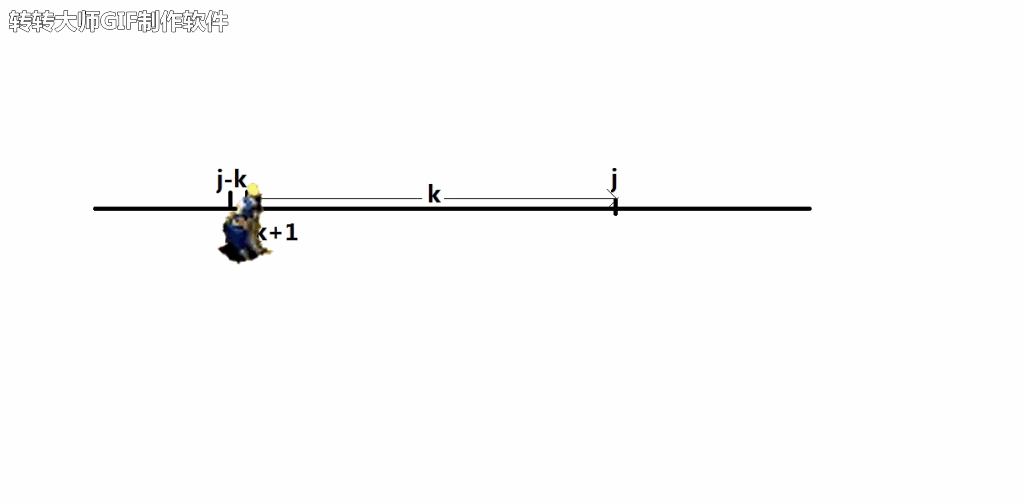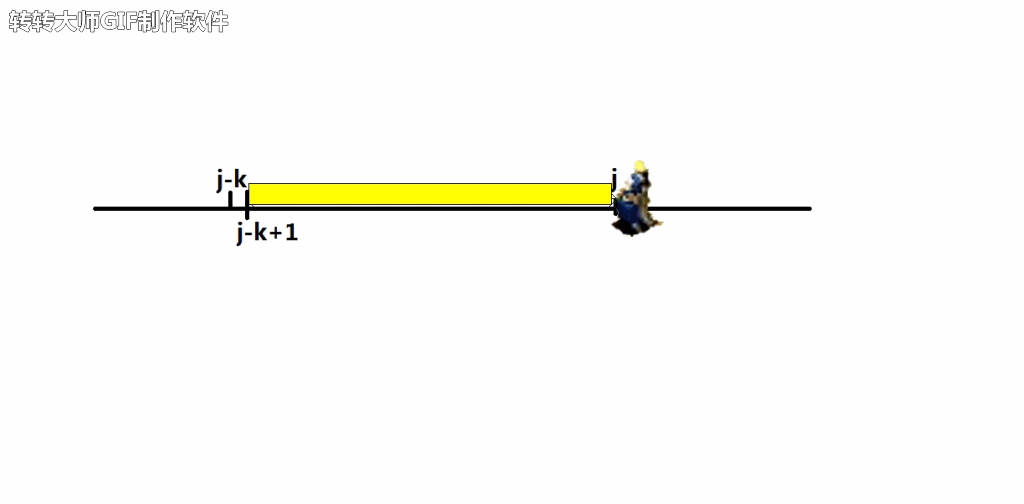
（不要问我为什么超时空传送可以传人，也不要问我为什么超时空传送能通过时间轴回到过去，更不要问我为什么左上角有水印，5555555~）
当然，关于蓝色工程师占领的时间轴是黄色的这件事，唯一的解释就是我们 中出 了个叛徒。

时间复杂度

大概是 $O(mn(2+logn))$

参考文献

老师讲完后，隔了一天我自己写出来的

C++ 代码

#include <bits/stdc++.h>
using namespace std;
//头文件和标准命名空间 

#define fi8(a,b) for(register int i=a;i<=b;++i)
#define fi2(a,b) for(register int i=a;i>=b;--i)
#define fj8(a,b) for(register int j=a;j<=b;++j)
#define fj2(a,b) for(register int j=a;j>=b;--j)
#define fv8(a,b) for(register int v=a;v<=b;++v)
#define fv2(a,b) for(register int v=a;v>=b;--v)
//for循环相关宏定义 f——for i——下标   8——↑    2——↓ 

#define X10(x) (x<<1)+(x<<3)    //快速x*10 
#define shu(x) (x>='0'&&x<='9') //判断是否是数字 
#define ch(x) x=getchar()       //getchar()简写 
inline int qread(int &a)
{
    int x=0,m=0;
    char ch(ch);
    while(!shu(ch)) m|=ch=='-',ch(ch);
    while(shu(ch)) x=X10(x)+(ch^48),ch(ch);
    a=m?-x:x;
    return a;
}
#define qrc(x,y) qread(x)*qread(y)  //p=m*n,所以这里直接利用函数返回值 
//快读以及相关宏定义 

struct workpiece    /*  工件 workpiece    */ 
{
    struct procedure    /*  工序 procedure    */
    {
        int machine_number; /*  机器号 machine_number  */
        int time;   /*  时间 time */
    }pro[21];
    int last;   /*  上一个 last    */
    int step;   /*  步骤 step */
}work[21];
int p,m,n,ans,id,cost,k;
int order[401];/*   顺序 order    */
bool bucket[21][100001];/*  桶 bucket    */
//定义全局变量 

#define g(x,y) work[x].pro[y]   //用宏定义函数的方式简写结构体 
#define gl(x) work[x].last      //同上 
#define gs(x) work[x].step      //同上 
#define num machine_number      //之后的所有num都代表 machine_number
#define bu bucket               //同理 
#define now order[i]            //同理 
//简写表 

int main()
{
    p=qrc(m,n); //利用自定义快读函数的返回值快速计算p 
    fi8(1,p) qread(order[i]);   //从1——m*m读入工作顺序 
    fi8(1,n)        //从1——n 
        fj8(1,m)    //从1——m 
            qread(g(i,j).num);  //依次读入work[i].pro[j].num,即第i个工件的第j道工序是work[i].pro[j].num号机器来完成的 
    fi8(1,n)        //从1——n 
        fj8(1,m)    //从1——m 
            qread(g(i,j).time); //依次读入work[i].pro[j].time,即第i个工件的第j道工序花费的时间是work[i].pro[j].time 
    //以上都是读入

    fi8(1,p)        //从1——m*m，根据工作顺序遍历 
    {
        gs(now)++;  // 步骤++ 

        id=g(now,gs(now)).num;      //方便表示num，同时不改变num的值 
        cost=g(now,gs(now)).time;   //同理

        fj8(gl(now)+1,100001)       //从目前步骤+1开始遍历 ，到时间轴的尽头 
        {

            if(!bu[id][j]) k++;     //计时装置k，顺着时间轴不断自增 
            else k=0;               //如果桶数组里[这台机器][此时此刻]有工作要做，表示这段时间内k不能作为工作的时间，所以就清空k，寻找新的空余时间 
            if(k==cost)             //当这台机器的空闲时间有足够当前工件加工的时间 
            {
                fv8(j-cost+1,j)     //j-cost+1表示v下标从刚刚k开始计时的地方到k正好到达j时的地方 
                    bu[id][v]=1;    //先在刚刚占用的时间上做标记 
                ans=max(j,ans);     //题目要求回答最少多长时间，最少我们已经用遍历法得到了，最少的总时长应该是最少的情况下时间轴上最长的那个 
                gl(now)=j;          //work[now].last=j表示当前的工件的上一个时间终点是j 
                break;              //跳出fj8，继续执行fi8 
            }
        }
        k=0;//不要忘记清零k，因为k表示当前工件的某段时间内的可用时间，下一个工件的初始可用时间为零 
    }
    printf("%d\n",ans);//输出花费的总时间 
}

fj8不是你们想的那个！
灵感来源于这个

懂的都懂！