瞎bb几句

写题解的主要原因就是害怕自己没有听懂
然后由于作者的记性不是很好，所以难一点的题会写一个题解当作备忘录用

郑重声明

本文的代码全部来自于y总动态规划第三讲中给出的代码
这篇题解只是记录我学习的过程中的一些肤浅的看法
代码并非是原创的,请勿见怪

正文

题目描述

给定n,m求出将你n$\times$m的长方形中有多少种方法使1$\times$2填满此长方形

思路

DP的状态f[i][j]在这一题中
i表示考虑到第i列
j表示这一列中的横着的放2$\times$1的格子个数
剩下的默认为填入竖着的格子
注意这里表示的放个都是一端在i-1列一端在i列
其中j是一个二进制数，在二进制表示1表示此格有格子

例子(仅考虑图中i和i-1列)

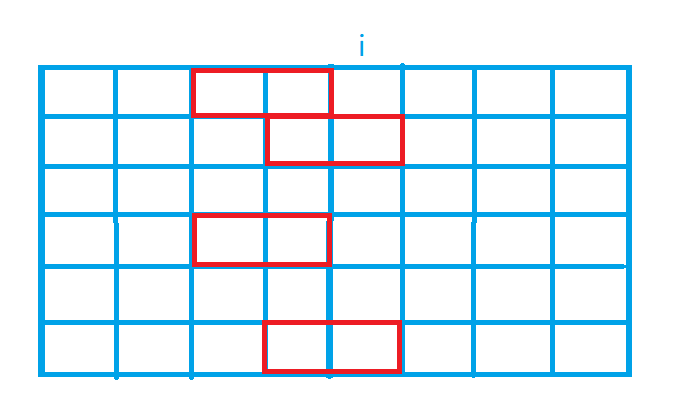{:height=”40%” width=”40%”}

那么此情况中j = $(100010)_2$

但是储存的时候就需要转换至十进制，也就是j = $(34)_{10}$、

所以当一个状态成立的时候需要两个条件
1. i-1列的格子和i列的格子不能再同一行
2. i-1列不能有连续奇数个空格(后面的st数组就是判定这个的)

C++代码

#include <algorithm>
#include <iostream>
#include <cstring>

using namespace std;

const int N = 12, M = 1 << N;

int n, m;
long long f[N][M];
bool st[M];

int main()
{
    while(cin >> n >> m, n || m)//n=m=0的时候会自动退出
    {
        memset(f, 0, sizeof(f));//记得初始化

        for(int i = 0; i < 1 << n; i ++ ) {
            st[i] = true;//先假设是可以的
            int cnt = 0;//计0的个数
            for (int j = 0; j < n; j++)//一个一个检测i的二进制的第j位是不是1
                if (i >> j & 1)//如果是, 看cnt是不是奇数
                {
                    if (cnt & 1) st[i] = false;//如果cnt是奇数,
                    cnt = 0;//cnt重新设为0，从头开始记0的个数
                }
                else cnt ++ ;//如果不是,往后看,同时0的个数加1

            if (cnt & 1) st[i] = false;//不要忘记最后有可能就没1了, 但是倒数有奇数个0
        }
        //dp
        f[0][0] = 1;
        for (int i = 1; i <= m; i ++ )//遍历第i列
            for(int j = 0; j < 1 << n; j ++ )
                for(int k = 0; k < 1 << n; k ++ )
                    if((j & k) == 0 && st[j | k])//判定此状态是否可以(见前面的两个条件)
                        f[i][j] += f[i - 1][k];

        cout << f[m][0] << endl;//输出结果
    }

    return 0;
}

一些解释

n,m: 题中的意思
f[N][M]: 解释中的意思，dp的状态
st[M]: 判定是否有奇数个0
前面的for循环就是初始化st数组(见此状态成立时的第二个条件)
后面的三重for循环才是dp的过程
最后也用到了st[j|k]也用到了