原文作者:莉墨lymoe
原题作者:莉墨 lymoe
他让我转过来的 qwq
题目灵感
当初其实是想考察一下“树上全源最短路”和“二分图染色”,想了很久也没想出怎么出。
最后就把这两个算法合到一块,就出现了这个题。
原本这个题难度并不高(刚开始数据 $ n $ 最大为 $1000$ (其实数据加强后,难度也不高QAQ)),后来WAAutoMaton发现了一个 $ O(n) $ 的算法,于是这个题就稍微难了一点。
Part 0-题目分析
分析题目可以发现,我们可以建立一个新图,新图中的点和原图中的点一一对应。如果 $ dis(u,v)\ge k $ 则在新图中把 $ u,v $ 相连。
那么新图中的任意一个“环”都对应一个满足题目条件的序列 $a_1 ,a_2,a_3,…,a_m$ 。
而如果新图中存在奇环,则为“无解”。
part 1-测试点1~10 40分
先用弗洛伊德算法求出全源最短路,建立新图。
我们知道不存在奇环的图为二分图。所以对新图进行二分图染色(或者用并查集判断二分图),若该图是二分图,则“有解”,若该图不是二分图,则“无解”。
part 2-测试点15~20 64分(40+24)
把弗洛伊德算法改用dfs求树上全源最短路即可。如果你嫌码量太小,使用tarjan、树剖、倍增等求lca的方法求最短路也可。
part 3-测试点11~14 16分
对于这一部分和下一部分的分数,已经不需要建立新图了,但是为了方便证明,我们还会说到这个新图。
我们来考虑一下这个退化成链的部分。
通过在纸上手造几个数据,我们可以发现新图的一个性质:若新图上存在奇数环,则一定存在三元环。
那么怎么证明呢?
由于链上的环跟链上的点编号无关,不妨设这个链上的点从左往右编号依次为 $ 1,2,3,…,n $ 。( $1,2$之间连边,$2,3$ 之间连边…以此类推)
设这个链对应的新图存在奇环 $ a_1,a_2,…,a_m $ ,且 $ m\not= 3 $ 。
不妨设 $ a_1 $ 为奇环中编号最小的点,$ a_x $ 为奇环中编号最大的点。
那么显而易见 $ dis(a_1,a_x)\ge k $ 。(因为如果奇环中距离最远的两个点距离都小于 $ k $ 的话,则新图上一定不存在这个奇环)
假设奇环上不存在一点 $ a_q $ 满足 $ dis(a_1,a_q) \ge k \text{ and } dis(a_1,a_x)\ge k$ ,则
$ \because dis(a_1,a_2)\ge k $
$ \therefore dis(a_2,a_x) < k $
$ \because dis(a_2,a_3) \ge k ,dis(a_2,a_x)<k$
$ dis(a_3,a_x)\ge k,dis(a_1,a_3)<k $
…
以此类推,可以用数学归纳法证明(这里就省略数学归纳的过程),$dis(a_{2p},a_x)<k $ ,$ dis(a_{2p+1},a_1)<k $ ,其中 $ p\in N^* $ 。那么可以发现,因为 $dis(a_{2p},a_x)<k $ ,所以无法构成包含 $ a_x $ 的奇环。
故产生矛盾,则奇环上存在一点满足 $ dis(a_1,a_q) \ge k \text{ and } dis(a_1,a_x)\ge k$ 。
则证明了存在奇数环就一定存在三元环。
那么接下来,我们可以猜测:若存在三元环,则存在包括 $ 1 $ 号点和 $ n $ 号点的三元环。
证明:
我们设三元环为 $ (a_1,a_2,a_3) $ 且 $ a_1<a_2<a_3 $ 。
$ \because dis(a_1,a_2)\ge k,a_1\ge1 $
$ \therefore dis(1,a_2)\ge k $
$ \because dis(a_2,a_3)\ge k,a_3\le n $
$ \therefore dis(a_2,n) \ge k $
所以存在三元环 $ (1,a_2,n) $ 满足条件 。
那么对于链的解法就显而易见了。我们只需要求一下前缀和,然后看看链上是否存在一点能与首尾构成三元环。
part 4-测试点21~25 100分
对于这部分分,我们可以采用类比法(类比part 3)。
同理我们先来证明,若存在奇数环,则存在三元环。
首先我们找到奇环里距离最远的两个点 $ a_1,a_x $ 。
假设奇环上不存在一点 $ a_q $ 满足 $ dis(a_1,a_q) \ge k \text{ and } dis(a_1,a_x)\ge k$ ,则
$ \because dis(a_1,a_2)\ge k $
$ \therefore dis(a_2,a_x) < k $
$ \because dis(a_2,a_3) \ge k ,dis(a_2,a_x)<k$
$ \therefore dis(a_3,a_x)\ge k,dis(a_1,a_3)<k $
…(若比较难理解可以自行画图)
所以与 part 3 相同,因为 $dis(a_{2p},a_x)<k $ ,所以无法构成包含 $ a_x $ 的奇环。
那么接下来,我们可以猜测:若存在三元环,则存在包括直径两个端点的三元环。
证明:
首先我们将树简化:
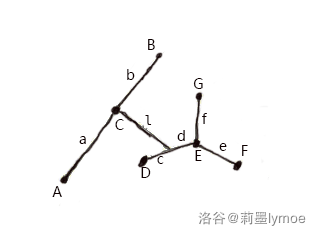
大写字母表示点,小写字母表示边,该简化图中边长可以为 $ 0 $ 。
$ AB $ 为树的直径, $ (D,F,G) $ 为直径外一三元环。
我们可以假设三元环上任意一点都不满足“到 $ A $ 的距离不小于 $ k $ 且到 $ B $ 的距离不小于 $ k $ ” 。
不妨设 $ (f+d)+l+b< k $ ,则
$ (f+d)+c \ge k$
$ \therefore b+l<c $
$ \therefore a+l+c>a+l+b+l\ge a+b $
则 $ dis(A,D)> dis(A,B) $ ,则 $ (A,B) $ 不为直径,产生矛盾。
所以三元环上存在一点满足“到 $ A $ 的距离不小于 $ k $ 且到 $ B $ 的距离不小于 $ k $ ”。
那么正解的算法也就显而易见了,只需要先求树的直径,再看看是否存在一点到直径两端距离不小于 $ k $ 。
最后贴出std:
#include<stdio.h>
#include<string.h>
#define MAXN 1000005
struct node
{
int eh;
}V[MAXN];
struct edge
{
int v;
int to;
int next;
}E[MAXN*2];
int tot;
int dis1[MAXN],dis2[MAXN];
void add_edge(int from,int to,int v)
{
E[++tot]=(edge){v,to,V[from].eh};
V[from].eh=tot;
}
void dfs(int i,int fa,int* dis)
{
int p;
for(p=V[i].eh;p;p=E[p].next)
{
if(E[p].to==fa) continue;
dis[E[p].to]=dis[i]+E[p].v;
dfs(E[p].to,i,dis);
}
}
int main()
{
int n,i,T,x,y,v,k,flag;
scanf("%d",&T);
while(T--)
{
memset(V,0,sizeof(V));
memset(E,0,sizeof(E));
tot=0;flag=1;
scanf("%d%d",&n,&k);
for(i=0;i<n-1;i++)
{
scanf("%d%d%d",&x,&y,&v);
add_edge(x,y,v);
add_edge(y,x,v);
}
dis1[1]=0;
dfs(1,0,dis1);x=1;
for(i=2;i<=n;i++)
{
if(dis1[i]>dis1[x]) x=i;
}
dis1[x]=0;
dfs(x,0,dis1);y=x;
for(i=1;i<=n;i++)
{
if(dis1[i]>dis1[y]) y=i;
}
dis2[y]=0;
dfs(y,0,dis2);
for(i=1;i<=n;i++)
{
if(dis1[i]>=k&&dis2[i]>=k) flag=0;
}
if(flag) printf("Yes\n");
else printf("Baka Chino\n");
}
return 0;
}


az
啊这,有点惊讶,楼上luogu红名
太强了!希望有一天能读懂这些大神的逻辑,并遇到同类题时能独立进行同样的推理