题目描述

Given an n x n binary grid, in one step you can choose two adjacent rows of the grid and swap them.

A grid is said to be valid if all the cells above the main diagonal are zeros.

Return the minimum number of steps needed to make the grid valid, or -1 if the grid cannot be valid.

The main diagonal of a grid is the diagonal that starts at cell (1, 1) and ends at cell (n, n).

样例

Example 1:

Input: grid = [[0,0,1],[1,1,0],[1,0,0]]
Output: 3

Example 2:

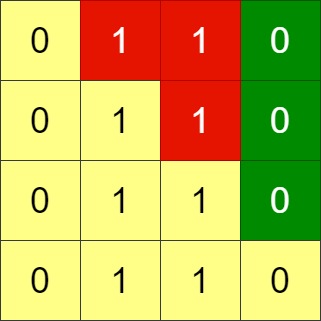
Input: grid = [[0,1,1,0],[0,1,1,0],[0,1,1,0],[0,1,1,0]]
Output: -1
Explanation: All rows are similar, swaps have no effect on the grid.

Example 3:

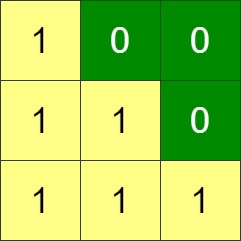
Input: grid = [[1,0,0],[1,1,0],[1,1,1]]
Output: 0

Constraints:

• n == grid.length
• n == grid[i].length
• 1 <= n <= 200
• grid[i][j] is 0 or 1

要让主对角线上的数字全是0，翻译过来就是从每一行的末尾开始的连续0的个数要满足：假如当前行是第i行（从0开始计数），那么连续的0的个数需要满足zeroNum[i] >= n - i - 1。

只能是行交换，意味着通过交换zeroNum内的数字使其满足条件。那么一个很自然的想法是zeroNum内的数字越大的越靠前，那么是不是排序并计算交换的次数（相当于计算逆序对次数，冒泡、归并、线段树搞一下），然后检验每一行是否满足条件即可呢？这种是存在问题的，比如最后三行末尾连续0的个数是3，4，5，此时无需交换也满足条件，但是排序则需要交换。

另外需要考虑的一点是，因为每次都是去寻找第一个能使当前行满足的zeroNum数字，是不是很类似首次适配的思想，是否可能存在第一个找到的数字满足了当前行的条件（设这一行为i），假如还有一行j也能让其满足条件，并且zeroNum[j] < zeroNum[i]，为什么不选择第j行这个更接近的呢？这是因为既然i和j行都能满足条件，那么当前行往下，第j行肯定也可以满足，并且第i行离当前行更近，交换的次数少，所以只需要每次选择第一个能使当前行末尾连续的0满足条件的数字即可。

因为需要统计每一行末尾连续的0的个数，最坏情况下$O(n^2)$，另外交换数字的最坏情况也是$O(n^2)$，空间复杂度$O(n)$。

class Solution {
public:
    int minSwaps(vector<vector<int>>& grid) {
        std::ios_base::sync_with_stdio(false);
        cin.tie(NULL);
        cout.tie(NULL);

        int n = grid.size();
        vector<int> zeroNum(n);

        for (int i = 0; i < n; ++i) {
            int j = n - 1;
            while (j >= 0 && grid[i][j] == 0) {
                ++zeroNum[i];
                --j;
            }
        }

        int res = 0;
        for (int i = 0; i < n - 1; ++i) {
            if (zeroNum[i] < n - i - 1) {
                int j = i + 1;
                while (j < n && zeroNum[j] < n - i - 1) ++j;
                if (j == n) return -1;
                while (j > i) {
                    std::swap(zeroNum[j], zeroNum[j - 1]);
                    --j;
                    ++res;
                }
            }
        }

        return res;
    }
};