题目描述

给你一个 n x n 的二进制网格 grid，每一次操作中，你可以选择网格的 相邻两行 进行交换。

一个符合要求的网格需要满足主对角线以上的格子全部都是 0。

请你返回使网格满足要求的最少操作次数，如果无法使网格符合要求，请你返回 -1。

主对角线指的是从 (1, 1) 到 (n, n) 的这些格子。

样例

输入：grid = [[0,0,1],[1,1,0],[1,0,0]]
输出：3

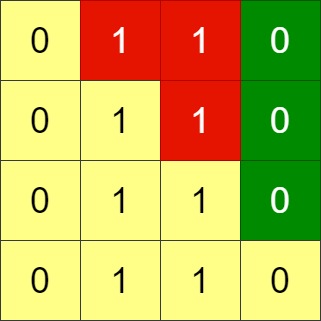
输入：grid = [[0,1,1,0],[0,1,1,0],[0,1,1,0],[0,1,1,0]]
输出：-1
解释：所有行都是一样的，交换相邻行无法使网格符合要求。

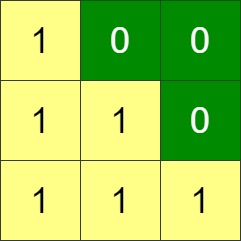
输入：grid = [[1,0,0],[1,1,0],[1,1,1]]
输出：0

限制

• n == grid.length
• n == grid[i].length
• 1 <= n <= 200
• grid[i][j] 要么是 0 要么是 1。

算法

(贪心) $O(n^2)$

1. 求出每一行的排名。排名指的是从最后一列开始第一个非 0 的位置。
2. 按照规则，第一行应该放排名小于等于 0 的，第二行应该放排名小于等于 1 的。以此类推，最后一行应该放排名小于等于 n - 1 的。
3. 从第一行开始，贪心的找到距离当前位置最近的一行，且其排名小于等于要求的排名。

时间复杂度

• 求出所有排名的时间复杂度为 $O(n^2)$，移动和排序的时间复杂度为 $O(n^2)$，故总时间复杂度也为 $O(n^2)$。

空间复杂度

• 需要额外 $O(n)$ 的空间存储排名。

C++ 代码

class Solution {
public:
    int minSwaps(vector<vector<int>>& grid) {
        const int n = grid.size();
        vector<int> rank(n);

        for (int i = 0; i < n; i++) {
            int j = n - 1;
            while (j >= 0 && grid[i][j] == 0) j--;
            rank[i] = j;
        }

        int ans = 0;
        for (int i = 0; i < n; i++) {
            int j = i;
            while (j < n && rank[j] > i) j++;
            if (j == n) return -1;

            ans += j - i;

            while (j > i) {
                rank[j] = rank[j - 1];
                j--;
            }
        }

        return ans;
    }
};