题目描述
You are given two sorted arrays of distinct integers nums1 and nums2.
A valid path is defined as follows:
- Choose array nums1 or nums2 to traverse (from index-0).
- Traverse the current array from left to right.
- If you are reading any value that is present in
nums1andnums2you are allowed to change your path to the other array. (Only one repeated value is considered in the valid path).
Score is defined as the sum of uniques values in a valid path.
Return the maximum score you can obtain of all possible valid paths.
Since the answer may be too large, return it modulo 10^9 + 7.
样例
Example 1:
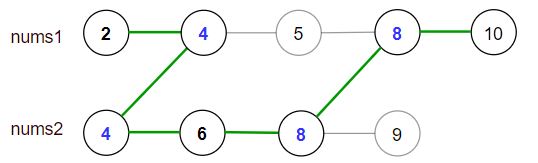
Input: nums1 = [2,4,5,8,10], nums2 = [4,6,8,9]
Output: 30
Explanation: Valid paths:
[2,4,5,8,10], [2,4,5,8,9], [2,4,6,8,9], [2,4,6,8,10], (starting from nums1)
[4,6,8,9], [4,5,8,10], [4,5,8,9], [4,6,8,10] (starting from nums2)
The maximum is obtained with the path in green [2,4,6,8,10].
Example 2:
Input: nums1 = [1,3,5,7,9], nums2 = [3,5,100]
Output: 109
Explanation: Maximum sum is obtained with the path [1,3,5,100].
Example 3:
Input: nums1 = [1,2,3,4,5], nums2 = [6,7,8,9,10]
Output: 40
Explanation: There are no common elements between nums1 and nums2.
Maximum sum is obtained with the path [6,7,8,9,10].
Example 4:
Input: nums1 = [1,4,5,8,9,11,19], nums2 = [2,3,4,11,12]
Output: 61
Constraints:
1 <= nums1.length <= 10^51 <= nums2.length <= 10^51 <= nums1[i], nums2[i] <= 10^7nums1andnums2are strictly increasing.
解法一:队列 + 贪心 + 双指针 + 前缀和
感觉这个题和前面比赛的Hard比较,也就是Medium的难度,其实这题很套路,对于有序列表:
- 如果是两个列表,数据范围是$10^3$,大概率就是动态规划,如果是$10^5$,那么大概率就是双指针
- 如果是多个有序列表,一般数据范围是$10^5$,基本上就是优先级队列
本题可以将每个数组进行切分,以第四个样例为例:
nums1 [1] (4) [5 8 9] (11) [19]
nums2 [2 3] (4) (11) [12]
其中()内的数字代表两个序列里相同的数字,每个[]内的数字是夹在两个()中间的数字,或者首尾两端的部分。()内的数字是必须要经过的,让结果存在区别的是[]内的数字,[]内的数字位置是连续的,所以可以用前缀和得到区间和。用两个队列存储两个序列里相同数字的下标,为了让每个序列的第一个[]好处理,两个队列里面都先加入数字0,显然两个队列的长度必然是相等的。如果队列的长度是1,意味着两个序列里没有相同的数字,那么直接计算两个数组的总和即可。
这样就可以计算两个()中间的[]产生的影响,留下每个数组末尾的[]单独处理。因为都只需要遍历一遍数组,时间复杂度$O(n)$,空间复杂度$O(n)$。
注意存在溢出,使用long long。
class Solution {
public:
int maxSum(vector<int>& nums1, vector<int>& nums2) {
std::ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int m = nums1.size(), n = nums2.size();
const int MODE = 1e9 + 7;
queue<int> q1, q2;
q1.push(0), q2.push(0);
vector<long long> prefixSum1(m + 1, 0), prefixSum2(n + 1, 0);
for (int i = 1; i <= m; ++i) prefixSum1[i] = prefixSum1[i - 1] + nums1[i - 1];
for (int i = 1; i <= n; ++i) prefixSum2[i] = prefixSum2[i - 1] + nums2[i - 1];
int pos = 0;
for (int i = 0; i < m; ++i) {
while (pos < n && nums2[pos] < nums1[i]) ++pos;
if (pos >= n) break;
if (nums1[i] == nums2[pos]) q1.push(i + 1), q2.push(pos + 1);
}
if (q1.size() == 1) return max(prefixSum1[m] % MODE, prefixSum2[n] % MODE);
long long res = 0;
while (q1.size() > 1) {
int tmp1 = q1.front(); q1.pop();
int tmp2 = q2.front(); q2.pop();
res = max(res + gap(tmp1, q1.front() - 1, prefixSum1) + nums1[q1.front() - 1],
res + gap(tmp2, q2.front() - 1, prefixSum2) + nums2[q2.front() - 1]);
}
res = max(res + gap(q1.front(), m, prefixSum1), res + gap(q2.front(), n, prefixSum2));
return res % MODE;
}
inline long long gap(int start, int end, vector<long long> & prefixSum)
{
return prefixSum[end] - prefixSum[start];
}
};
解法二:对于解法一的空间优化,其实也可以不必计算前缀和,只需要用两个变量即可。空间复杂度优化到$O(1)$。
class Solution {
public:
int maxSum(vector<int>& nums1, vector<int>& nums2) {
std::ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int m = nums1.size(), n = nums2.size();
const int MODE = 1e9 + 7;
long long res = 0, sum1 = 0, sum2 = 0;
int pos1 = 0, pos2 = 0;
while (pos1 < m && pos2 < n) {
if (nums1[pos1] < nums2[pos2]) sum1 += nums1[pos1++];
else if (nums1[pos1] > nums2[pos2]) sum2 += nums2[pos2++];
else {
res += max(sum1, sum2) + nums1[pos1++];
++pos2;
sum1 = sum2 = 0;
}
}
if (pos1 < m) {
for (int i = pos1; i < m; ++i) sum1 += nums1[i];
}
if (pos2 < n) {
for (int i = pos2; i < n; ++i) sum2 += nums2[i];
}
res += max(sum1, sum2);
return res % MODE;
}
};

