我在做这道题时还不会二项式定理呢！
想了一会儿，我发现这个式子可以拆成：
(ax+by)(ax+by)…(ax+by)
也就是在每一个括号了面都选一个数，乘起来。
刚好要求的是x^n * b^m前的系数。
然后利用数形结合，就可以将原来的公式变成这个样子：

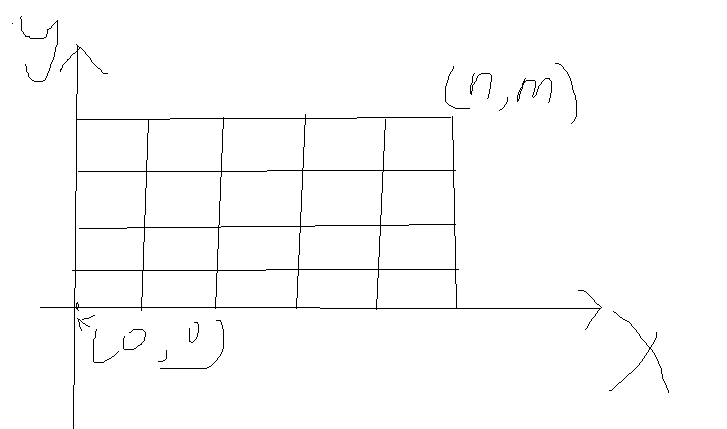
我们要求的是从原点到(n,m)的路径条数，直接用dp即可（跟快的话可以用组合数）

#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
const int N = 1010, P = 10007;
int a, b, k, n, m;
int f[N][N];
int main() {
    cin >> a >> b >> k >> n >> m;
    for (int i = 0; i <= n; i++) f[i][0] = 1;
    for (int j = 0; j <= m; j++) f[0][j] = 1;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++) 
            f[i][j] = (f[i - 1][j] + f[i][j - 1]) % P;
    int ans = f[n][m];
    a %= P;
    for (int i = 1; i <= n; i++) ans = (ans * a) % P;
    b %= P;
    for (int i = 1; i <= m; i++) ans = (ans * b) % P;
    cout << ans << endl; return 0;
}