题目描述

给你一个 rows x cols 的矩阵 grid 来表示一块樱桃地。
grid 中每个格子的数字表示你能获得的樱桃数目。

你有两个机器人帮你收集樱桃，
机器人 1 从左上角格子 (0,0) 出发，机器人 2 从右上角格子 (0, cols-1) 出发。

请你按照如下规则，返回两个机器人能收集的最多樱桃数目：

从格子 (i,j) 出发，机器人可以移动到格子 (i+1, j-1)，(i+1, j) 或者 (i+1, j+1) 。
当一个机器人经过某个格子时，它会把该格子内所有的樱桃都摘走，
然后这个位置会变成空格子，即没有樱桃的格子。
当两个机器人同时到达同一个格子时，它们中只有一个可以摘到樱桃。
两个机器人在任意时刻都不能移动到 grid 外面。
两个机器人最后都要到达 grid 最底下一行。

示例1

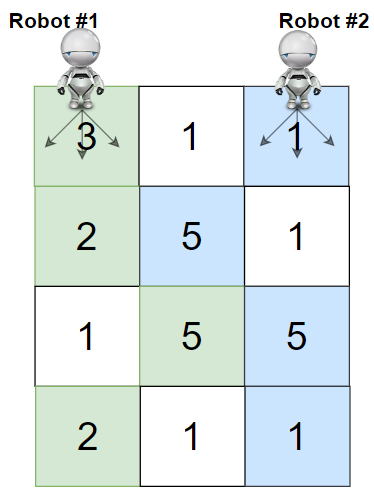
输入：grid = [[3,1,1],[2,5,1],[1,5,5],[2,1,1]]
输出：24
解释：机器人 1 和机器人 2 的路径在上图中分别用绿色和蓝色表示。
机器人 1 摘的樱桃数目为 (3 + 2 + 5 + 2) = 12 。
机器人 2 摘的樱桃数目为 (1 + 5 + 5 + 1) = 12 。
樱桃总数为： 12 + 12 = 24 。

示例2

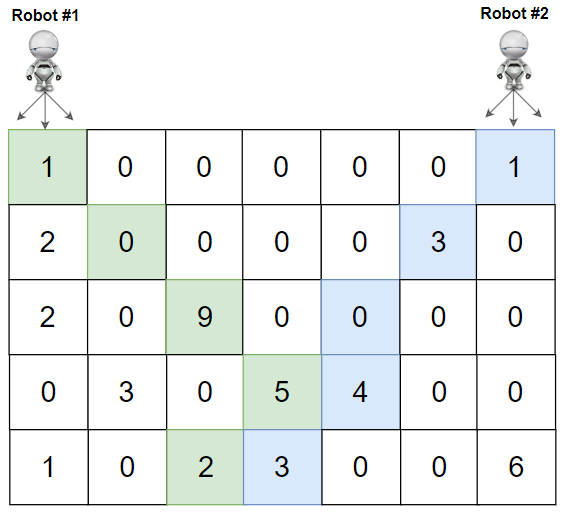
输入：grid = [[1,0,0,0,0,0,1],[2,0,0,0,0,3,0],[2,0,9,0,0,0,0],[0,3,0,5,4,0,0],[1,0,2,3,0,0,6]]
输出：28
解释：机器人 1 和机器人 2 的路径在上图中分别用绿色和蓝色表示。
机器人 1 摘的樱桃数目为 (1 + 9 + 5 + 2) = 17 。
机器人 2 摘的樱桃数目为 (1 + 3 + 4 + 3) = 11 。
樱桃总数为： 17 + 11 = 28 。

示例 3：
输入：grid = [[1,0,0,3],[0,0,0,3],[0,0,3,3],[9,0,3,3]]
输出：22

示例 4：
输入：grid = [[1,1],[1,1]]
输出：4

提示：

rows == grid.length
cols == grid[i].length
2 <= rows, cols <= 70
0 <= grid[i][j] <= 100 

算法1

这里使用双DP
两者同时行动 所以肯定是在同一横坐标上
dp[k][x1][x2];
k表示处于的横坐标轴 x1 是机器人1的竖坐标 x2是机器人2的竖坐标，指示的dp表示能获取的最多樱桃
初始值要注意机器人所在的点赋值樱桃值，其余可复制最小值，可以避免计算一些机器人本来无法达到的位置。

本题和acwing 1027 方格取数 比较类似

C++ 代码

class Solution {
public:


int dp[100][100][100];

int checkVal = 0;


bool Check(int x)
{
    if (x >= 0 && x < checkVal)
        return true;

    return false;
}

int cherryPickup(vector<vector<int>>& grid) {
    memset(dp, 0, sizeof dp);

    if (grid.size() == 0 || grid[0].size() == 0) return 0;
    checkVal = grid[0].size();

    for(int k=0;k<100;k++){
        for(int i=0;i<100;i++){
            for(int j =0;j<100;j++){
                dp[k][i][j] = -9999999;
            }
        }
    }


    if(grid[0].size() - 1 != 0)
        dp[0][0][grid[0].size() - 1] = grid[0][0] + grid[0][grid[0].size() - 1];
    else 
        dp[0][0][grid[0].size() - 1] = grid[0][0] ;

    int ans = 0;

    for (int k = 1; k < grid.size(); k++) {
        for (int y1 = 0; y1 < grid[0].size(); y1++) {
            for (int y2 = 0; y2 < grid[0].size(); y2++) {
                int val = grid[k][y1];
                if (y1 != y2) val += grid[k][y2];

                if (Check(y1) && Check(y2))
                    dp[k][y1][y2] = max(dp[k][y1][y2], dp[k - 1][y1][y2] + val);
                if (Check(y1+1) && Check(y2))
                    dp[k][y1][y2] = max(dp[k][y1][y2], dp[k - 1][y1+1][y2]+val);
                if (Check(y1-1) && Check(y2))
                    dp[k][y1][y2] = max(dp[k][y1][y2], dp[k - 1][y1- 1][y2]+val);

                if (Check(y1) && Check(y2-1))
                    dp[k][y1][y2] = max(dp[k][y1][y2], dp[k - 1][y1][y2-1]+val);
                if (Check(y1+1) && Check(y2 - 1))
                    dp[k][y1][y2] = max(dp[k][y1][y2], dp[k - 1][y1 + 1][y2-1]+val);
                if (Check(y1-1) && Check(y2 - 1))
                    dp[k][y1][y2] = max(dp[k][y1][y2], dp[k - 1][y1 - 1][y2-1]+val);

                if (Check(y1) && Check(y2 + 1))
                    dp[k][y1][y2] = max(dp[k][y1][y2], dp[k - 1][y1][y2+1]+val);
                if (Check(y1+1) && Check(y2 + 1))
                    dp[k][y1][y2] = max(dp[k][y1][y2], dp[k - 1][y1 + 1][y2+1]+val);
                if (Check(y1-1) && Check(y2 + 1))
                    dp[k][y1][y2] = max(dp[k][y1][y2], dp[k - 1][y1 - 1][y2+1]+val);

                if (k == grid.size() - 1 && Check(y1) && Check(y2))
                    ans = max(ans, dp[k][y1][y2]);
            }
        }
    }

    return ans;
}
};