原题连接

题目描述

求 N 个节点的无向连通图有多少个，节点有标号，编号为1~N。

例如下列图示，三个节点的无向连通图共4个。

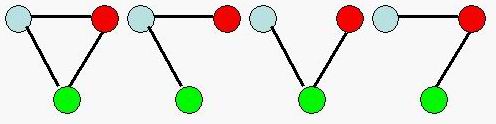
输入格式

输入包含多组测试数据。

每组数据包含一个整数N。

当输入为0时，表示输入终止。

输出格式

每组测试数据输出一个结果，每个结果占一行。

数据范围

$1 \le N \le 50$

输入样例：

1
2
3
4
0

输出样例：

1
1
4
38

解题报告

题意理解

对于一道题目而言,理解题意是关键,那么这道题目的题意描述,其实就是已经精简过了,那么我就不重复了,意思就是$N$个节点的无向联通图,一共有多少个.

算法确定

这道题目的目标要求,要求出一共有多少方案,不难想到和计数类型的算法有关.

再加上这道题目数学气息比较浓厚,数据范围也不是直接用数学求解的复杂度的样子.$O(1)$或者说$(Olog(n))这种类型的.

综上所述,我们可以把目光放到计数型DP的上面.

算法分析

计数型动态规划不同于其他动态规划算法,它通常都是要把一个问题分成多个不重不漏的子问题,类似于分治一样处理.

对于一个连通图而言,划分似乎不是什么好处理的事情,那么我们不妨继续想到构造法.

毕竟对于一道题目而言,当我们不能从划分求解了,那么我们就得想到构造,因为这两个算法的目标一样,只不过算法实现恰恰相反.

划分和构造的关系,就像前缀和和差分,倍增和二分,都是一种互逆算法,目的是一样,实现的方法确实相反的.

性质求解

构造法,其实往往也和我们之前所说的容斥原理有关.

在这道题目中,我们发现题目要我们构造无向连通图,但是显然我们似乎不好构造出来,所以说我们不妨考虑,我么能不能使用之前的容斥的思想.

合法的无向连通图=所有无向连通图个数-无向不连通的无向图.

综上所述,我们现在的目的,只要两点,那就是求解所有连通图总数,以及无向不连通图的个数.

所有连通图的个数,显然是有公式求出来了,这一点在学习图论基础的时候,我们就学过,但是我们这里还是详细说明.

N个点的无向图总数求解公式如下所示.
$$ 2^{N*(N-1)/2} $$
一个数学公式,总是让人难以第一时间理解,所以我们需要中文文字说明.

因为对于一个无向图而言,它最多有$(N*(N-1)/2)$条边.

因为首先对于$N$个点而言,我们都可以和其他$N-1$点链接,但是又因为A链接B,会计算一条,B链接A的时候也会计算一条,所以我们要方案数除以二.

再加上对于一条边而言,我们可选,可不选,所以说我们的所有连通图的求解公式如下所示.
$$ 2^{N*(N-1)/2} $$

接下来我们的目标放在了求解无向不连通图个数

对于一个不联通的无向图而言,它是由K个连通块构成的.$(k \ge 2)$

上面这个性质对于这道题目而言非常重要,因为我们不连通的无向图,是由若干个连通块构成的,那么只需要求解连通块个数>1的无向图总数

连通块个数>1的无向图,我们并不在意它由多少块构成,我们只需要知道,当前这个图,它的连通块个数大于1,不是无向连通图就可以了.

我们对于一张不合法的图而言,我们显然是只需要,枚举一个连通块,然后剩下的点构成任意无向图即可.因此此时连通块个数已经大于1了.

综上所述,我们不妨枚举标号为$i$的点,它所在的连通块节点个数有$K$个,然后在除了它以外的$N-1$个节点中,选出剩下的$K-1$个节点.

那么现在我们已经构造好了一个连通块,它一共有$C_{N-1}^{K-1}$种枚举方法,那么接下来我们可以将最后剩余的节点,构成任意无向图即可.

任意无向图的公式,其实上面求解所有无向图的公式$2^{N*(N-1)/2}$,只不过你当前剩余的节点个数是$(N-K)$而已.
$$ 2^{(i-j) \times (i-j-1)/2} $$

公式总结

综上所述,我们可以设置$F[i]$表示为$i$个节点的无向连通图个数,它的状态转移方程为.
$$ F[i]=2^{i \times (i-1)/2}-\sum_{j=1}^{i-1}{F[j] \times C_{i-1}^{i-1} \times 2^{(i-j)\times (i-j-1)/2}} $$
初始值$F[1]=1$.最后的目标为$F[N]$

还有这道题目最恶心的地方是要高精度,所以这道题目难度又恶心了一倍.

出题人相信这道,思路精简,代码优秀,题意简单的题目,可以给你完美的人生,留下浓黑的一笔.

代码解释

#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N=110;
const int M=1100;
int n,m,i,j,k;
struct bign
{
    int a[M],len;
} f[N],power[N];
inline bign operator / (const bign &x,const int y)
{
    bign now;
    memset(now.a,0,sizeof now.a);
    now.len=0;
    int ns=0;
    for(int i=x.len; i>=1; i--)
    {
        ns=ns*10+x.a[i];
        now.a[i]=ns/y;
        ns%=y;
        if(!now.len && now.a[i]) now.len=i;
    }
    return now;
}
inline bign operator + (const bign &x,const bign &y)
{
    bign now;
    memset(now.a,0,sizeof now.a);
    for(int i=1; i<=max(x.len,y.len); i++)
    {
        now.a[i]+=x.a[i]+y.a[i];
        now.a[i+1]=now.a[i]/10;
        now.a[i]%=10;
    }
    now.len=max(x.len,y.len);
    if(now.a[now.len+1]) 
        now.len++;
    return now;
}
inline bign operator * (const bign &x,const bign &y)
{
    bign now;
    memset(now.a,0,sizeof now.a);
    for(int i=1; i<=x.len; i++)
        for(int j=1; j<=y.len; j++)
        {
            now.a[i+j-1]+=x.a[i]*y.a[j];
            now.a[i+j]+=now.a[i+j-1]/10;
            now.a[i+j-1]%=10;
        }
    now.len=x.len+y.len-1;
    if(now.a[now.len+1]) 
        now.len++;
    return now;
}
inline bign C(int x,int y)
{
    bign tot,temp;
    tot.len=1;
    tot.a[1]=1;
    for(int i=y,j=1; j<=x; i--,j++)
    {
        int t=i;
        temp.len=0;
        while(t)
        {
            temp.a[++temp.len]=t%10;
            t/=10;
        }
        tot=tot*temp/j;
    }
    return tot;
}
inline void print(const bign &x)
{
    for(int i=x.len; i>=1; i--)
        printf("%d",x.a[i]);
    printf("\n");
}
inline void init()
{
    for(int i=1; i<=50; i++)
    {
        ll temp=((ll)(1)<<i)-1;
        while(temp)
        {
            power[i].a[++power[i].len]=temp%10;
            temp/=10;
        }
    }
    f[1].len=1;f[1].a[1]=1;f[2].len=1;f[2].a[1]=1;
    for(int i=3; i<=50; i++)
        for(int j=1; j<=i-1; j++)
            f[i]=f[i]+C(j-1,i-2)*f[j]*f[i-j]*power[j];//预处理
}
int main()
{
    init();
    while(scanf("%d",&n) && n) 
        print(f[n]);
    return 0;
}