题目描述

给出一些不同颜色的盒子，盒子的颜色由数字表示，即不同的数字表示不同的颜色。
你将经过若干轮操作去去掉盒子，直到所有的盒子都去掉为止。
每一轮你可以移除具有相同颜色的连续 k 个盒子（k >= 1），这样一轮之后你将得到 k*k 个积分。
当你将所有盒子都去掉之后，求你能获得的最大积分和。

提示

• 1 <= boxes.length <= 100
• 1 <= boxes[i] <= 100

样例

输入：boxes = [1,3,2,2,2,3,4,3,1]
输出：23
解释：
[1, 3, 2, 2, 2, 3, 4, 3, 1] 
----> [1, 3, 3, 4, 3, 1] (3*3=9 分) 
----> [1, 3, 3, 3, 1] (1*1=1 分) 
----> [1, 1] (3*3=9 分) 
----> [] (2*2=4 分)

算法1

(记忆化搜索)

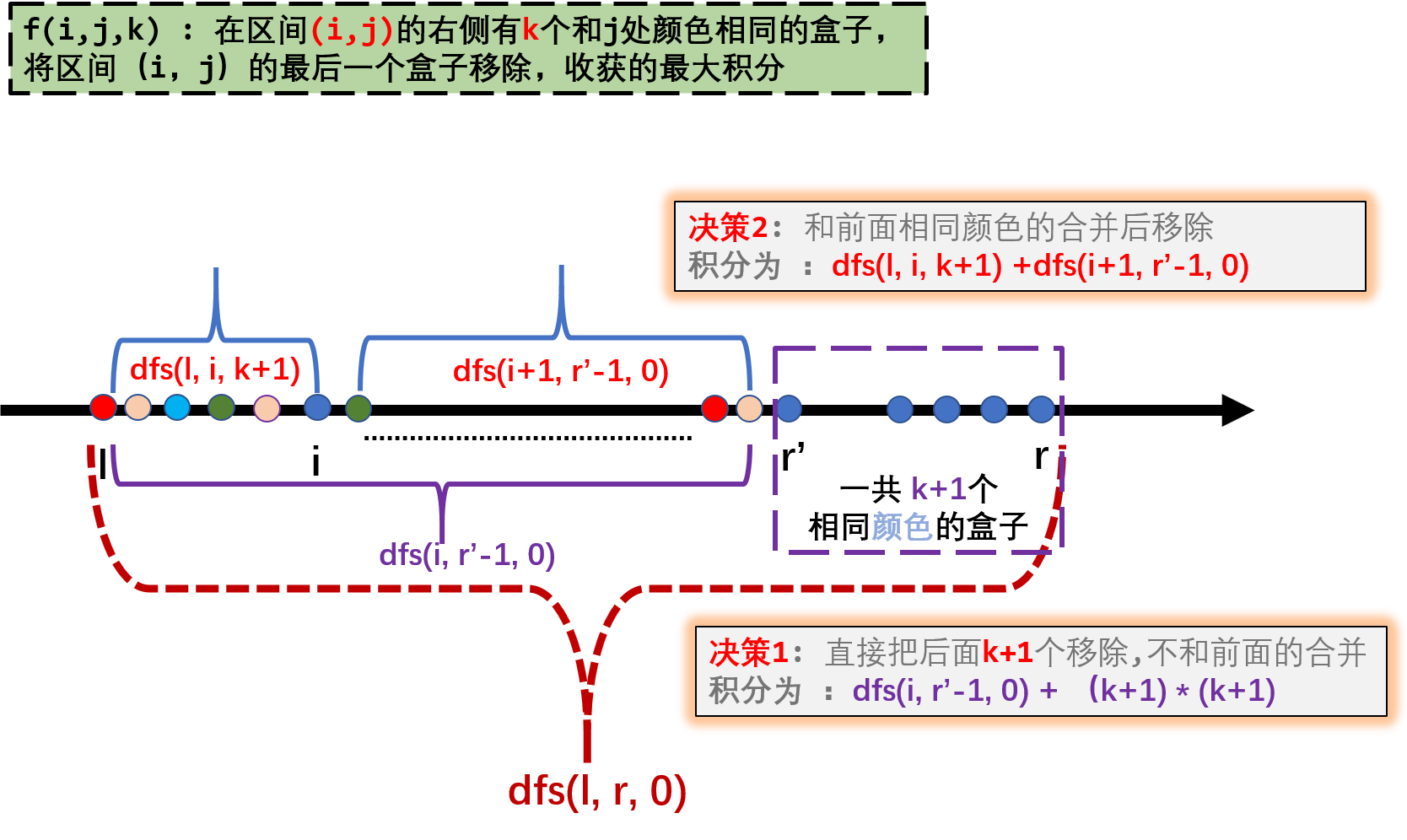
对于每个盒子，我们有两种选择

• 决策1 ：直接把相邻相同的全部移除
• 决策2 ：把不相邻的合并后一起移除，当然在合并前，把中间破环他们相邻的所有盒子要移除

dfs(l, r，k)

• 当前处理的区间[l,r], 目的是要移除区间最右边的盒子也就是box[r]
• k表示该区间外也就是其右边，有连续k个和boxer[r]相同颜色的盒子可以一起删除
• f(i,j,k) 表示进行上述操作后的最大收益

C++ 代码

class Solution
{
    int f[101][101][101];
    vector<int> b;

public:
    int removeBoxes(vector<int>& boxes)
    {
        b = boxes;
        int n = b.size();
        memset(f, 0 ,sizeof(f));
        return dfs(0, n - 1,0);  
    }

    int dfs(int l,int r,int k)  // [l, r]区间内, 目前能够删除k个与 b[r]相同颜色盒子的的最大收益
    {
        if(l > r) return 0;

        while(l < r && b[r]== b[r-1]) r--, k++; 
        //k说明b[r]后面有K个和b[r]相同的值
        //也就是 能连续删除 k + 1 b[r]

        if(f[l][r][k] > 0)  return f[l][r][k]; // 如果已经有答案 直接返回，否则再进行计算

        // 决策1 直接删除
        f[l][r][k] = dfs(l, r - 1, 0) + (k + 1) * (k + 1); // 删除k + 1个， 递归处理前面的区间[l, r-1]

        // 决策2 在【l, r -1】区间找到和b[r]相等的，合并起来一起删除 
        for(int i = l; i < r;i++)  // 找的了 为b[i] ,于是将[l, r -1 ] 分成了 2段 [l, i] [ i + 1, r - 1]
            if(b[i]==b[r])   //
                f[l][r][k] = max(f[l][r][k], dfs(l,i,k + 1) + dfs(i + 1,r - 1, 0));

        return f[l][r][k];
    }
};