分析

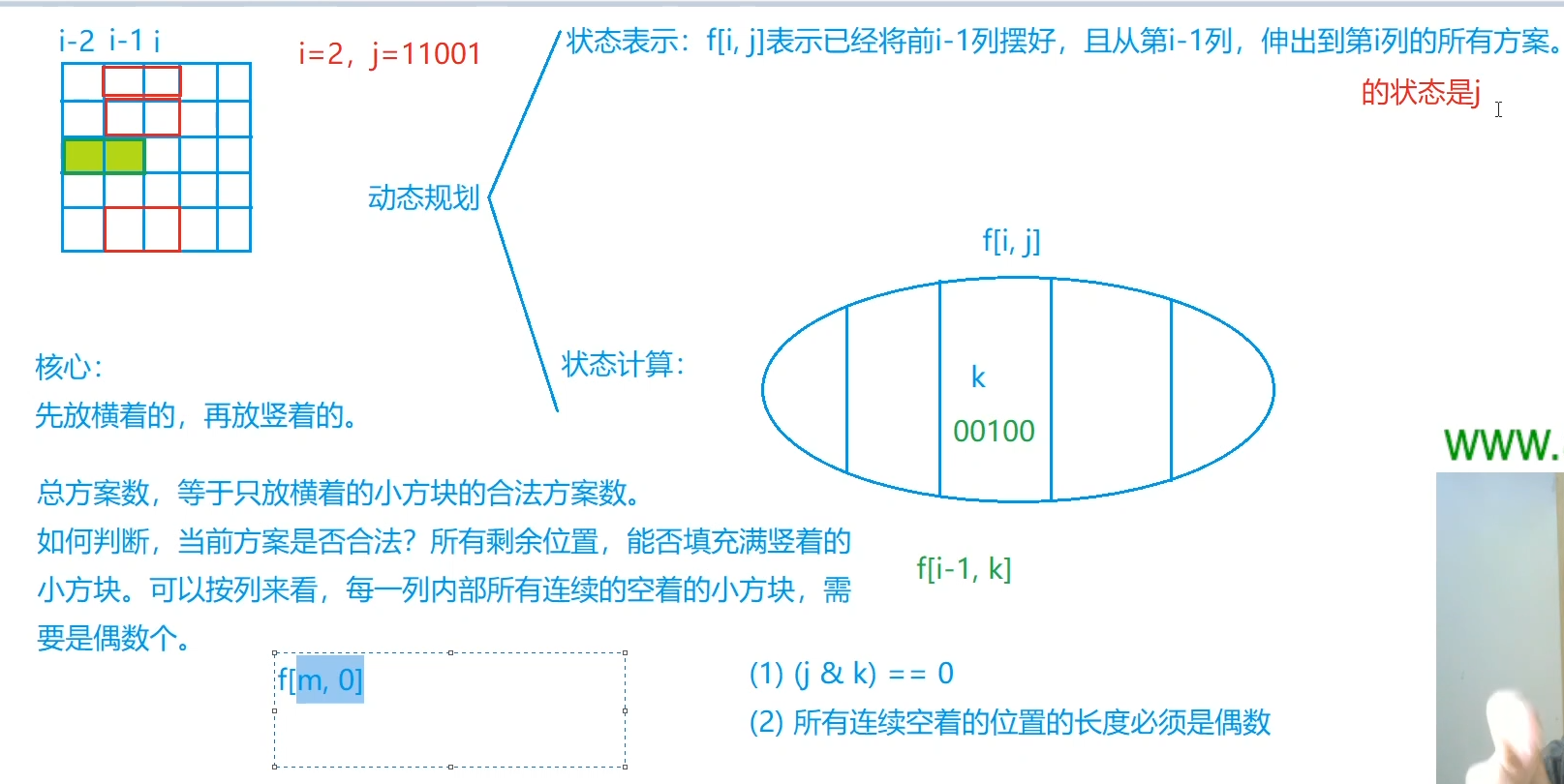
集合:前i-1列已经摆好,且前i-1列摆放的横着的砖头延伸到第i列的状态j的方案数(第i-1列为砖块的起始位置)
条件:1.空格必须是偶数个 2.不能存在冲突
可以用k来表示第i-2列延伸到第i-1列的状态,枚举j的状态之后再一一枚举k的状态,如果此时j的状态已经固定,即第i-1列和第i列的状态已经固定了,但是第i-2列到i-1列的状态没有固定,所以可以枚举第i-2列延伸到第i-1列的状态,如果符合条件那么就可以证明能从第i-2列延伸到第i-1列的状态k可以转移到从第i-1列延伸到第i列的状态k,所以此时可以得到状态转移方程:
f[i][j]=f[i][j]+f[i-1][k];

暴力版

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 12, M = 1 << N;

int n, m;
long long f[N][M];
bool st[M];

int main()
{
    while (cin >> n >> m, n || m)
    {
        for (int i = 0; i < 1 << n; i ++ )
        {
            int cnt = 0;
            st[i] = true;
            for (int j = 0; j < n; j ++ )
                if (i >> j & 1)
                {
                    if (cnt & 1) st[i] = false;
                    cnt = 0;
                }
                else cnt ++ ;
            if (cnt & 1) st[i] = false;
        }

        memset(f, 0, sizeof f);
        f[0][0] = 1;
        for (int i = 1; i <= m; i ++ )
            for (int j = 0; j < 1 << n; j ++ )
                for (int k = 0; k < 1 << n; k ++ )
                    if ((j & k) == 0 && st[j | k])
                        f[i][j] += f[i - 1][k];

        cout << f[m][0] << endl;
    }
    return 0;
}

优化版

提前枚举出符合条件的状态

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>

using namespace std;

typedef long long LL;

const int N=12,M=1<<N;//因为要处理出结果,所以N=12;(从第零列开始计算)

LL f[N][M];//f[i][j]中i表示的是列数,而j表示的是方案数与状态
vector<int> state[M];//例如state[j]存储的就是j|k后满足条件的k的集合,可以减少时间复杂度
bool st[M];//例如st[j]中,j如果存在连续奇数个零,那么st[j]=false,如果是只有连续偶数个零,那么st[j]=ture;

int main()
{
    int n,m;
    while(cin>>n>>m,n||m)//本体有多种数据
    {
        for(int i=0;i<1<<n;i++)//算出每个二进制是存在连续奇数个零还是不存在连续奇数个零
        {
            int cnt=0;
            bool is_value=true;
            for(int j=0;j<n;j++)
            if(i>>j&1)//如果为1,那么开始判断是连续奇数个零还是连续偶数个零
            {
                if(cnt&1)
                //如果二进制的最后一个数为1,那么一定为奇数,反之为偶数,因为二进制其他位的值都为偶数
                {
                    is_value=false;
                    break;
                }
                cnt=0;
            }
            else cnt++;
            if(cnt&1) is_value=false;
            st[i]=is_value;
        }
        //st数组储存的是一个二进制数中是否有连续奇数个零,如果有则为false,反之则为true

        for(int i=0;i<1<<n;i++)//将所有满足条件的状态都预处理出来,减少时间复杂度
        {
            state[i].clear();
            for(int j=0;j<1<<n;j++)
            if((i&j)==0&&st[i|j])
            state[i].push_back(j);
        }

        memset(f,0,sizeof(f));//**每次循环之后,上一次的数据应该清空**
        f[0][0]=1;
        /*
         dp[i][j]的含义是第i-1列的砖块延伸到第i列的状态j,因为第-1列压根不存在,所以
         从第-1列的砖块延伸到第0列的状态j为00000,只有这一种方案,所以f[0][0]的方案数
         为1;
        */
        for(int i=1;i<=m;i++)
         for(int j=0;j<1<<n;j++)
          for(auto k : state[j])
          f[i][j]+=f[i-1][k];
        /*
        当状态f[i][j]和f[i-1][k]不冲突的时候说明状态f[i][j]可以由状态f[i-1][[k]
        一步转移过来，而f[i-1][k]中存放的是从初始状态到f[i-1][k]的方案数，故到
        达状态f[i][j]的方案中一定包含路径：初始状态-->f[i-1][k]-->f[i][j], 所有
        f[i][j] = f[i][j] + f[i-1][k]
        */
        cout<<f[m][0]<<endl;
        //f[m][0]代表的是从第m-1列伸到m列的状态是零,即没有砖头伸到第m列的所有方案数
        //注:本代码是从第0列排列到第m-1列

    }

    return 0;
}

更为详细的解析:

集合:前i-1列已经摆好,且前i-1列摆放的横着的砖头延伸到第i列的状态j的方案数(第i-1列为砖块的起始位置)
条件:1.空格必须是偶数个 2.不能存在冲突
用k来表示第i-2列的砖块延伸到第i-1列的状态,j来表示从第i-1列延伸到第i列的方案,（因为砖块横着摆放的长度是2,所以k也就是把砖块头放在第i-2列的状态,因为长度为2,所以砖块尾会延伸到第i-1列,j的表示也是同理）.如果此时j的状态是已经固定了的,即前i-1列摆放着的横着的砖头延伸到第i列的状态已经确定了,但是第i-2列横着摆放的砖头延伸到第i-1列的状态还没有确定,那么我们就开始枚举第i-2列摆放横着的砖头延伸到第i-1列的状态,即k的状态,这里我们用二进制来表示k的状态,因为横着的砖头摆放完后,便要摆放竖着的砖头,所以必须要确保能装下竖着的摆放砖头.因为竖着的砖头的长度为1,所以横着摆放砖头的状态中间必须保证要有偶数个空位才行.那么如何判断呢?
首先第i-1列存有的砖头是j和k状态的叠加,因为砖块头和砖块尾巴都在第i-1列上,又因为j和k都是用二进制表示的,所以j和k的二进制数的1叠加后(即进行异或操作后)，必须存有连续偶数个0,如果符合条件那么就可以证明能从第i-2列延伸到第i-1列的状态k可以转移到从第i-1列延伸到第i列的状态k,所以此时可以得到状态转移方程:
f[i][j]=f[i][j]+f[i-1][k];
问题:为什么不需要判断j和k的状态呢?
因为第f[i-1][k]表示的是前i-2列已经摆好,且前i-2列摆放的横着的砖头延伸到第i-2列的状态j的方案数,所以f[i-1][k]存的必定是合法的方案数,所以第i-2行的空位肯定是偶数位.(f[i-1,k]状态判断的合法条件是第i-3列的状态k与第i-1列的状态j的在第i-2列中的异或值的连续零为偶数).那么j呢,如果第i列枚举完后,那么就开始判断第i+1列了,因为第i+1列判断的是第i列中第i-1列延伸到第i的砖块的状态和第i列延伸到第i+1列的状态的异或值不发生冲突,所以第j也无需判断

如果存在错误，还望各位大佬指点QWQ