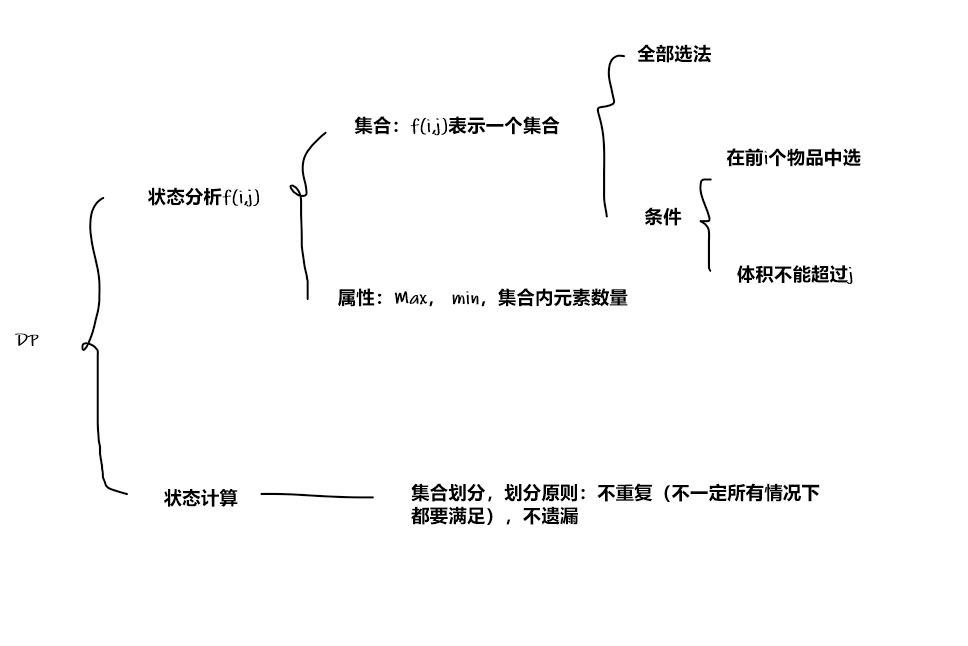
多重背包
关于多重背包的朴素做法,在基础课里有讲到
for (int i = 1; i <= n; ++ i) {
int v, w, s;
cin >> v >> w >> s;
for (int j = 0; j <= m; ++ j)
for (int k = 0; k <= s && k * v <= j; ++ k)
f[i][j] = max(f[i][j], f[i - 1][j - k * v] + k * w);
}
那么如何用单调队列来优化呢?
r : 背包容积j除以物品体积v的余数
r=背包容积(j)%物品体积(v)
对于物品i而言,放进背包的话背包的容积就会减少vi,如果物品i的数量足够多的话,那么用他来填背包的时候,填到无法再放下物品i的时侯,背包剩余的空间为j−k∗vi,也就是j%vi。所以说用1~k个物品i来填背包,背包的剩余容积为:r、r+vi、r+2vi、r+3vi、···、j−vi、j。
由于一个物品i占vi的体积,所以当背包体积在j−vi、j−vi+1、j−vi+2、···、j−1的时候是装不进去一个新的物品i的,所以我们只看r、r+vi、r+2vi、r+3vi、···、j−vi、j这些情况就可以。
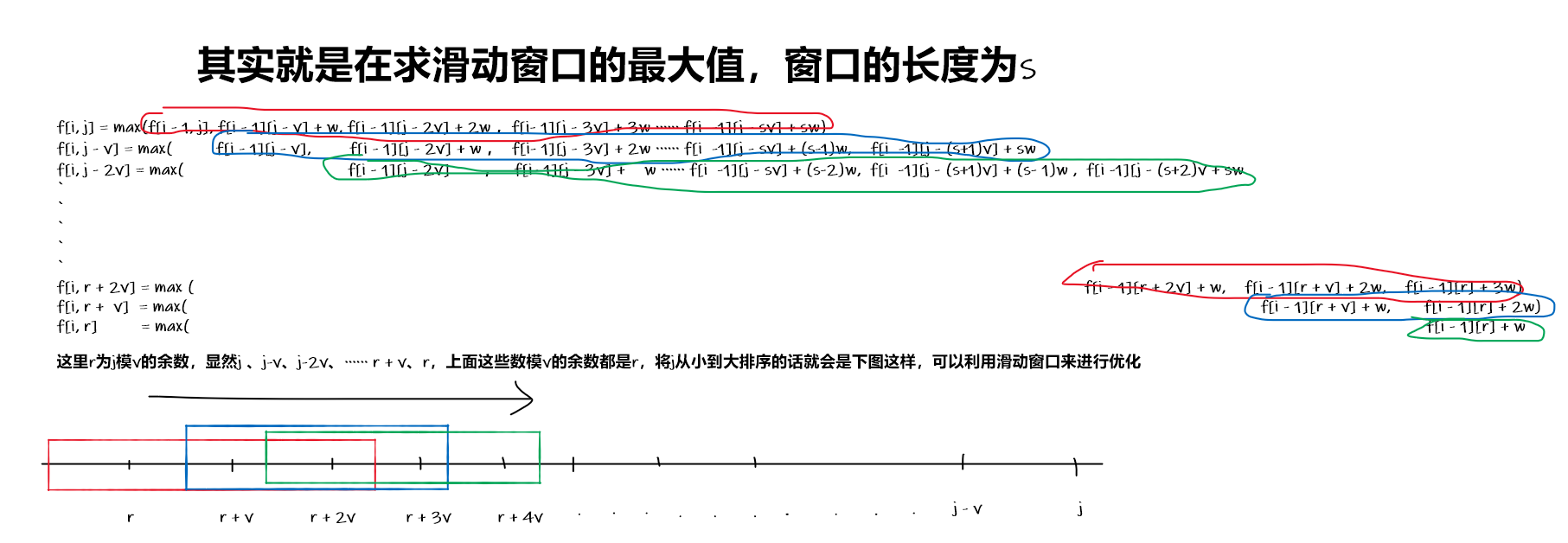
可以看到,当背包体积j在减少v的时候,窗口右滑了一格,而题目要求的是这个窗口内元素的的最大值,如果用朴素的DP的话,就会重新再算一遍这个窗口内所有的元素,但是这个窗口只去掉了一个旧元素,加入了一个新元素,其他元素并没有发生变化,所以没有必要再一次计算多余的元素。可以用一个单调队列来维护一个窗口的最大元素。关于单调队列来做滑动窗口的题可以看基础班的视频。
这里不用for(int j = 0; j <= m; j ++)······来枚举背包的容积,而是用r、r+vi、r+2vi、r+3vi、···、j−vi、j来枚举背包的容积。假设一个物品的体积为v,那么背包容积j除以物品体积v的余数为0~(v−1)可以用以下代码来枚举背包容积。
for (int j = 0; j < v; ++ j) {
for (int k = j; k <= m; k += v) {
}
一些变量的意义:
- s :滑动窗口的长度(或者说s∗v是滑动窗口的长度),s是滑动窗口内元素个数。
- q[ ]:存的是窗口内单调递减的元素的下标,队头元素是窗口内最大的元素的值的下标,比如当前维护队列内有两个元素,且
f[i][j - v] + w > f[i][j - 2v]那么队头元素q[hh] = j - v而第二个元素q[hh + 1] = j - 2v (k - q[hh]) / v * w:由于q[hh]存的是j - sv,而这里用k表示体积那么一共有(k - q[hh]) / v个此物品,他的价值为(k - q[hh]) / v * w
#include <iostream>
using namespace std;
const int N = 1010, M = 20010;
int q[M]; // s的最大值为20000,v的最小值为1,所以队列里面最多是会有200010个元素的
int n, m;
int f[N][M];
int main(){
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
cin >> n >> m;
for (int i = 1; i <= n; ++ i) {
int v, w, s;
cin >> v >> w >> s;
for (int j = 0; j < v; ++ j) {
int hh = 0, tt = -1;
for (int k = j; k <= m; k += v) {
if (hh <= tt && q[hh] < k - s * v) ++ hh; // 判断单调队列中的最大元素是否已经滑出窗口
f[i][k] = f[i - 1][k]; // 不放物品i
if (hh <= tt) f[i][k] = max(f[i][k], f[i - 1][q[hh]] + (k - q[hh]) / v * w); // 放物品i
while (hh <= tt && f[i - 1][q[tt]] + (k - q[tt]) / v * w <= f[i - 1][k]) -- tt; // 更新单调的队列
q[++ tt] = k; // 更新单调的队列
}
}
}
cout << f[n][m] << endl;
return 0;
}
优化成一维:我发现其实优化不优化时间是几乎一样的,个人认为写二维的比较容易理解,没有必要盲目追求优化成一维。

#include <iostream>
#include <cstring>
using namespace std;
const int N = 1010, M = 20010;
int q[M]; // s的最大值为20000,v的最小值为1,所以队列里面最多是会有200010个元素的
int n, m;
int f[M], g[M];
int main(){
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
cin >> n >> m;
for (int i = 1; i <= n; ++ i) {
int v, w, s;
cin >> v >> w >> s;
for (int j = 0; j < v; ++ j) {
int hh = 0, tt = -1;
memcpy(g, f, sizeof f); // 用g[]来保存上一次的更新
for (int k = j; k <= m; k += v) {
if (hh <= tt && q[hh] < k - s * v) ++ hh;
if (hh <= tt) f[k] = max(f[k], g[q[hh]] + (k - q[hh]) / v * w);
while (hh <= tt && g[q[tt]] + (k - q[tt]) / v * w <= g[k]) -- tt;
q[++ tt] = k; // 更新单调的队列
}
}
}
cout << f[m] << endl;
return 0;
}


我宣布,这才是最好的题解
同学,你好,我这句话没看明白,可以帮忙解释一下吗
由于一个物品i占vi的体积,所以当背包体积在j−vi、j−vi+1、j−vi+2、⋅⋅⋅、j−1的时候是装不进去一个新的物品i的,所以我们只看r、r+vi、r+2vi、r+3vi、⋅⋅⋅、j−vi、j这些情况就可以。
背包体积在j-vi的时候为啥不能装进一个新的物品i呢,感觉很怪啊,装完一个vi以后刚好是j啊
最强题解,没有之一!
好详细,爱了爱了
窗口的长度是不是应该是s+1呢感觉
while (hh <= tt && f[i - 1][q[tt]] + (k - q[tt]) / v * w <= f[i - 1][k]) -- tt; // 更新单调的队列这行代码怎么理解?帮助队头确定入队的几个体积中选谁的价值最大,若新入体积中的价值没有队头的大,队头就不变,否则就会把队头指向新入的体积,具体是把小于等于队头,且在后面的一个一个踢出去,再让队头队头指向新入体积
图示那里 +w 标注错了, 后面三行都多加了一个w,比如更新 f[i][r] 的时候,因为 r<v, 此时 r 的空间一定放不下一个物品的体积,只能上一个状态 f[i−1][r] 转移过来(不放第 i 个物品),w写错的地方我用红笔标注出来了,希望楼主后期可以更正一下。
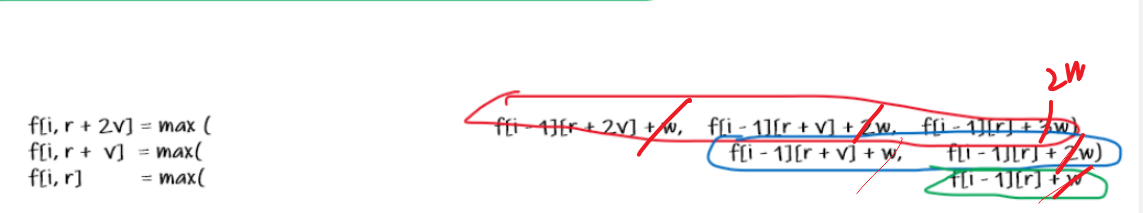
yyds,你这里滑动窗口里的下标比y总写的还要简洁,爱了
妙啊,看了好多题解越来越清晰了
好伟大啊
大佬们 ,为什么最终答案是dp[m], 每一类都互不相关,最终不应该枚举dp[1~m]的最大值吗?
写的很好,找了好几个题解,就你的能看懂…
if (hh <= tt && q[hh] < k - s * v) ++ hh; 这一句一直不理解,能给我讲一下吗,k是当前背包体积,减去sv之后就是负数了啊
这里把k理解成
滑动窗口的末尾位置的下标可能好理解点,然后减去长度s * v就得到这个“窗口”的起始位置的下标,如果超出了,就把这个头元素给踢出去。