题目描述
给定一张 n 个点的带权无向图,点从 0~n-1 标号,求起点 0 到终点 n-1 的最短Hamilton路径。 Hamilton路径的定义是从 0 到 n-1 不重不漏地经过每个点恰好一次。
输入格式
第一行输入整数n。
接下来n行每行n个整数,其中第i行第j个整数表示点i到j的距离(记为a[i,j])。
对于任意的x,y,z,数据保证 a[x,x]=0,a[x,y]=a[y,x] 并且 a[x,y]+a[y,z]>=a[x,z]。
输出格式
输出一个整数,表示最短Hamilton路径的长度。
数据范围
1≤n≤20
0≤a[i,j]≤107
样例
输入样例:
5
0 2 4 5 1
2 0 6 5 3
4 6 0 8 3
5 5 8 0 5
1 3 3 5 0
输出样例:
18
状态压缩DP分析:
1.本题思路
假设:一共有七个点,用0,1,2,3,4,5,6来表示,那么先假设终点就是5,在这里我们再假设还没有走到5这个点,且走到的终点是4,那么有以下六种情况:
first: 0–>1–>2–>3–>4 距离:21
second: 0–>1–>3–>2–>4 距离:23
third: 0–>2–>1–>3–>4 距离:17
fourth: 0–>2–>3–>1–>4 距离:20
fifth: 0–>3–>1–>2–>4 距离:15
sixth: 0–>3–>2–>1–>4 距离:18
如果此时你是一个商人你会走怎样的路径?显而易见,会走第五种情况对吧?因为每段路程的终点都是4,且每种方案的可供选择的点是0~4,而商人寻求的是走到5这个点的最短距离,而4到5的走法只有一种,所以我们选择第五种方案,可寻找到走到5这个点儿之前,且终点是4的方案的最短距离,此时0~5的最短距离为(15+4走到5的距离).(假设4–>5=8)
同理:假设还没有走到5这个点儿,且走到的终点是3,那么有一下六种情况:
first: 0–>1–>2–>4–>3 距离:27
second: 0–>1–>4–>2–>3 距离:22
third: 0–>2–>1–>4–>3 距离:19
fourth: 0–>2–>4–>1–>3 距离:24
fifth: 0–>4–>1–>2–>3 距离:26
sixth: 0–>4–>2–>1–>3 距离:17
此时我们可以果断的做出决定:走第六种方案!!!,而此时0~5的最短距离为(17+3走到5的距离)(假设3–>5=5)
在以上两大类情况之后我们可以得出当走到5时:
1.以4为终点的情况的最短距离是:15+8=23;
2.以3为终点的情况的最短距离是:17+5=22;
经过深思熟虑之后,商人决定走以3为终点的最短距离,此时更新最短距离为:22。
当然以此类推还会有以1为终点和以2为终点的情况,此时我们可以进行以上操作不断更新到5这个点的最短距离,最终可以得到走到5这个点儿的最短距离,然后再返回最初的假设,再依次假设1,2,3,4是终点,最后再不断更新,最终可以得出我们想要的答案
2.DP分析:
用二进制来表示要走的所以情况的路径,这里用i来代替
例如走0,1,2,4这三个点,则表示为:10111;
走0,2,3这三个点:1101;
状态表示:f[i][j];
集合:所有从0走到j,走过的所有点的情况是i的所有路径
属性:MIN
状态计算:如1中分析一致,0–>·····–>k–>j中k的所有情况
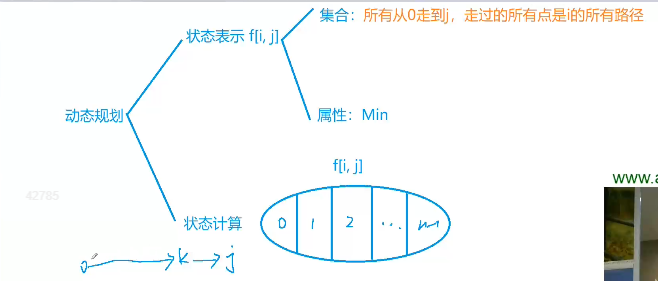
状态转移方程:f[i][j]=min(f[i][j],f[i-(1<<j)][k]+w[k][j])
代码:
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=20,M=1<<N;
int f[M][N],w[N][N];//w表示的是无权图
int main()
{
int n;
cin>>n;
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
cin>>w[i][j];
memset(f,0x3f,sizeof(f));//因为要求最小值,所以初始化为无穷大
f[1][0]=0;//因为零是起点,所以f[1][0]=0;
for(int i=0;i<1<<n;i++)//i表示所有的情况
for(int j=0;j<n;j++)//j表示走到哪一个点
if(i>>j&1)
for(int k=0;k<n;k++)//k表示走到j这个点之前,以k为终点的最短距离
if(i>>k&1)
f[i][j]=min(f[i][j],f[i-(1<<j)][k]+w[k][j]);//更新最短距离
cout<<f[(1<<n)-1][n-1]<<endl;//表示所有点都走过了,且终点是n-1的最短距离
//位运算的优先级低于'+'-'所以有必要的情况下要打括号
return 0;
}


大佬这题解写的 tql
雪豹闭嘴
雪豹闭嘴
雪豹闭嘴
雪豹闭嘴
雪豹闭嘴
雪豹闭嘴
雪豹闭嘴
雪豹闭嘴
不要给我发绿尸寒啊,丁真珍珠先生
怎么在哪里都能看到芝士丁真
雪豹闭嘴
雪豹闭嘴
雪豹闭嘴,来口瑞克五>.<
雪豹闭嘴
雪豹闭嘴
雪豹闭嘴
雪豹闭嘴
雪豹闭嘴
雪豹闭嘴
/眼(00)丁真,鉴定为:%
雪豹闭嘴
雪豹闭嘴
雪豹闭嘴
$ 雪豹闭嘴 $
闭嘴雪豹
雪豹闭嘴
雪豹闭嘴
雪豹闭嘴
雪豹闭嘴
雪豹闭嘴
雪豹闭嘴
雪豹闭嘴
雪豹闭嘴
雪豹闭嘴
纪念,打卡 , ✌语言丁真,鉴定为c++
雪豹闭嘴
雪豹闭嘴
雪豹闭嘴
???什么梗
看楼主头像
雪豹闭嘴
雪豹闭嘴
雪豹闭嘴
雪豹闭嘴
雪豹闭嘴
雪豹闭嘴
雪豹闭嘴
雪豹闭嘴
雪豹闭嘴
雪豹闭嘴
雪豹闭嘴
雪豹闭嘴雪豹闭嘴
雪豹闭嘴
雪豹闭嘴
雪豹闭嘴
雪豹闭嘴
雪豹闭嘴
雪豹闭嘴
丁真 哥哥
雪豹请闭嘴
雪豹闭嘴
雪豹闭嘴
雪豹闭嘴
雪豹闭嘴
说一个细节的我的理解,由于状态从0到1<<n,是从小到大遍历的,求这个状态最值的过程中,用到的都是把某一位1变成0的状态,而把1变成0之后这个二进制数一定会变小,那么它就一定是算好的(因为从小往大遍历的每个状态)
同学们加油
哈哈哈,好多好多冒充y总的
请问为什么, 先循环状态, 再循环所有点
你要先算出来这个状态的所有落脚点的值,再算下个状态的值
为啥要算完所有状态呀
计算出 0 到 2^n - 1 递增的状态上不同终点与路径的最小值,后面状态的计算需要用到前面状态的结果
为什么当k大于j还能算呢
比如一个二进制11111111,他中间有很多个1,但是他不一定是从0到1再到2再到3最后到n-1这个点,他里面的顺序可以是打乱的
懂啦,谢谢解释
搞不懂为什么第一个题,初始化为零,这个题初始化为正无穷
因为这题是求最小值
好的
请问,状态转移的时候,k是可以等于j的吗? 感觉很奇怪。
不能,但是转移也不影响结果 如果k=j 那么从k转移到j 等于自己到自己 w[k][j] = 0
f[i][j] = min(f[i][j], f[i - (1 << j)][j] + w[k][j]; 那么如果当k == j的话, f[i][j] = min(f[i][j], f[i - (1 << j][j] + 0; 这里的i - (1 << j) 不包含j点,它就没有经过j点,那这样不会产生混乱吗?
兄弟你这个状态方程写错了哦f[i - (1 << j)][k]这个二维的地方是k不是j
在这里可以j,这种情况下,dp[i-(1<<j)][j]是一开始设定的极大值,因为这个点在之前的循环中没有被修改过
当k==j时,转移方程变为f[i][j] = min(f[i][j], f[i - (1 << j)][j] + w[j][j]),因为f[i - (1 << j)][j]是不合定义的状态,因此仍然是初始最大值,而w[j][j]值为0,因此加和仍为初始最大值,在min函数执行时不会造成任何影响(相当于跳过了)。
其实加入if(k == j) continue;可以得出依旧是可以ac的,因此效果和跳过一样
不可以,但是你可以找个例子代入看一看,然后就会发现k=j时根本不会参与运算自己也不会被运算为别的数
这句话是什么意思啊 大佬
i的第j位为1,意思就是点j在状态i里这个应该是判断i的j+1位是否为1吧
意思就是枚举状态 i 中所有路径经过 j 点的 j
# 好牛逼
## 谢谢大佬
tql我竟然懂了
6
大佬, 请问最后的答案为什么是f[(1<<n)-1][n-1]
1<<n 是二进制表示首位是1后面都是0, 比如 1<<2 的二进制表示是 100
这样 f[(1<<n)-1][n-1] 表示的是 最后走到 n-1 个点, 走过的点的状态是 100000… (等于只走了第n-1个点)
我理解, 正确的答案应该是 最后走到n-1个点, 走过的点的状态是 11111… 这种状态才对,
你倒数第二行说错了, f[(1<<n)-1][n-1] 表示的是最后走到n-1 个点,走过的点的状态就是1111.....11(一共n个1);因为1 <<n 等于1后面n个零,你再减去1不就是一共n个1了
牛逼!位运算太妙了,减去二进制的1,就是最高位为0,低位全1,恰好就是从0走到n-1的状态!
就我异或这题为什么不能用图的算法解决吗
我也是这题一看应该是最短路啊
tle啊,你说为什么叫状压(以空间换时间)
朴素O(n!)规模最大是n=10
最短Hamilton路径是要求每个点都走到而且距离最短,但是最短路不一定走过了每个点
想知道,为什么最后的结果就是f[(1<<n)-1][n-1],为什么最小的路径一定是以n-1这个点结尾呢,有大佬能指点一下吗
这个是题目要求的啊,n-1就是终点
哦哦,没注意,以为是找到一个任意的汉密尔顿环路的最小值,谢谢
这为什么就状态压缩了呢,不太明白状态压缩什么意思
将路径的状态用二进制压缩
一直搞不懂状态压缩是什么意思……
就是用二进制数来表示状态,比如说0001代表整数1,就代表走过了1这个点。
大概是明白了,看来得多刷几次
for里面加的两个if有什么用
表示这个点可以走到
谢谢
是如何保证一定从起点0出发的呢?
题目有说的
我想问的是代码如何保证是从0出发的
因为他的初始状态是0已经经过的状态
哦哦好的好的,感谢感谢,%%%
不用谢
兄弟,我这里还没太明白,可以帮忙讲解一下吗,为啥能保证起点0出发的呢
老师,您好,请教一下呢,为什么f[1][0]=0就能保证是从0出发的呢,那我写f[0][0]=0或者f[2][0]=0可不可以保证是从0出发的呢
你没理解f[1][0]的含义,前一个数表示状态,1的二进制表示为00…0001,二进制每位表示有没走过,此时0的位置上为1就表示走过了,且0到0距离最小值为0,所以这样初始化,视频讲的很清楚了你可以再看看
请问一下,后面如果更新状态时候是从0更新的,比如f[111][2]是从f[011][0]更新过来的,会不会导致最后的哈密顿图不是从0开始呢
枚举的前一个状态已经被算过是因为 [ i-(1<<j ] 这个状态比 [ i ] 小,而 i 是从小到大枚举的,是这样吗?
对,这里是二进制的特殊性,当我们对任何一个是1的位操作时,我们必然已经枚举它之前的所有状态
first: 0–>1–>2–>3–>4 距离:21。这个距离是怎么算的呀,题目意思给我看蒙了。
这个不是算的,这个是我假设的
这个就是根据样例算出来的,楼主时间长了也忘了估计
题目意思就是第一个行第一列表示0到0点距离,第一行第二列表示0到1的距离,后面就是表示0到2的距离
我刚刚推半天推不对我还一直以为我题意理解错了
哈哈哈哈
我也推半天呢,无奈把题解丢给chat-gpt,gpt按照题解的推理也对不上,看到这条评论我心情只有…
很详细O~一下子就懂了~
# 谢谢大佬!学到了很多~
# 涨姿势了
走0124三个点为什么是11101,023为什么又是1101?