题目描述

在代号为 C-137 的星球上，Rick 发现如果他将两个球放在他新发明的篮子里，它们之间会形成特殊形式的磁力。Rick 有 n 个空的篮子，第 i 个篮子的位置在 position[i]，Morty 想把 m 个球放到这些篮子里，使得任意两球间 最小磁力最大。

已知两个球如果分别位于 x 和 y，那么它们之间的磁力为 |x - y|。

给定一个整数数组 position 和一个整数 m，请你返回最大化的最小磁力。

样例

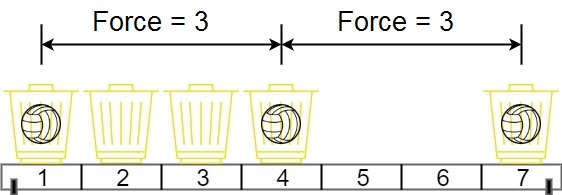
输入：position = [1,2,3,4,7], m = 3
输出：3
解释：将 3 个球分别放入位于 1，4 和 7 的三个篮子，两球间的磁力分别为 [3, 3, 6]。最小磁力为 3。
我们没办法让最小磁力大于 3。

输入：position = [5,4,3,2,1,1000000000], m = 2
输出：999999999
解释：我们使用位于 1 和 1000000000 的篮子时最小磁力最大。

限制

• n == position.length
• 2 <= n <= 10^5
• 1 <= position[i] <= 10^9
• 所有 position 中的整数 互不相同。
• 2 <= m <= position.length

算法

(贪心，二分答案) $O(n (\log n + \log M))$

1. 我们可以看到，限制的最小磁力越大，则越难找到一组位置。答案存在与否与最小磁力是成单调关系的。首先将位置从小到大排序。
2. 由此，可以二分最终的最小磁力，二分的区间时 [1, maxP - minP]。
3. 判定一个最小磁力 threshold 能否被满足时，可以贪心。固定第一个球放在第一个位置，其余的球则放到与上一个球满足 threshold 要求的且最近的位置。
4. 每次判定 mid+1 是否能满足要求，如果可以，则 l = mid + 1。否则 r = mid。

时间复杂度

• 排序的时间复杂度为 $O(n \log n)$。
• 二分每次判定的时间复杂度为 $O(n)$。
• 故总时间复杂度为 $O(n (\log n + \log M))$，其中 $M$ 为最大位置与最小位置的差值。

空间复杂度

• 仅需要常数的额外空间。

Go 代码

func maxDistance(position []int, m int) int {
    sort.Ints(position)
    n := len(position)

    l, r := 1, position[n-1]-position[0]
    for l < r {
        mid := (l + r) / 2
        if check(position, n, mid+1, m) {
            l = mid + 1
        } else {
            r = mid
        }
    }

    return l
}

func check(position []int, n, threshold, m int) bool {
    last := position[0]
    tot := 1

    for i := 1; i < n; i++ {
        if position[i]-last < threshold {
            continue
        }

        tot++
        if tot == m {
            return true
        }

        last = position[i]
    }

    return false
}