题目描述

给定一个链表，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。

说明：不允许修改给定的链表。

样例

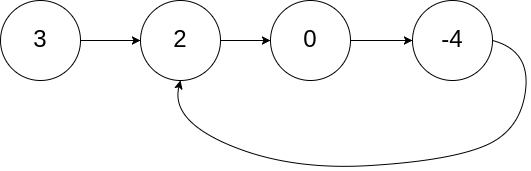
输入：head = [3,2,0,-4], pos = 1
输出：tail connects to node index 1
解释：链表中有一个环，其尾部连接到第二个节点。

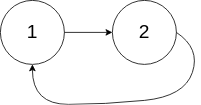
输入：head = [1,2], pos = 0
输出：tail connects to node index 0
解释：链表中有一个环，其尾部连接到第一个节点。

输入：head = [1], pos = -1
输出：no cycle
解释：链表中没有环。

进阶：
你是否可以不用额外空间解决此题？

算法分析

通过 LeetCode 141. 环形链表 的题解可以判断出环形链表是否存在环，而这题是需要找出 $pos$ 的位置

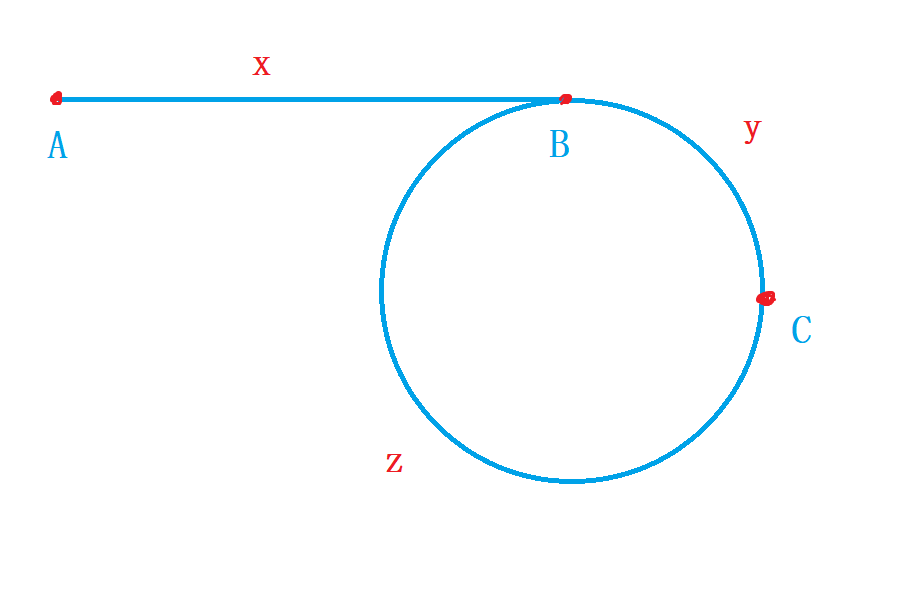
$fast$ 指针从原点每次走 2 步， $slow$ 指针从原点每次走 1 步

1、当链表不存在环，$fast$ 指针一定会事先走到 $null$，则 $pos = -1$

2、当链表中存在环时，如图所示，$A$ 点是起点，$B$ 点是入口，$C$ 点是两个指针的第一次相遇点，假设 $A$ 到 $B$ 长度是 $x$， $B$ 到 $C$ 长度是 $y$，$C$ 到 $B$ 长度是 $z$，假设当 $slow$ 指针走到 $B$ 点时，$fast$ 指针走到 $C$ 点，$fast$ 指针在环内兜了 $n$ 圈，则由于 $fast$ 走过的路程是 $slow$ 的 2 倍，因此在第一次相遇时，$slow$ 走过的路程是 $x + y$，$fast$ 走过的路程是$x + (y + z) * n + y$，因此 $x + (y + z) * n + y = 2(x + y)$，由于 $y + z$ 为环形的一圈，尽量凑在一起，因此化简为 $x = (y + z) * (n - 1) + z$

3、又化简后的等式可知，$x$ 与 $z$ 只相差圈数，因此从 $C$ 点走 $x$ 步一定会到达 $B$ 点，等价于从 $A$ 点走到 $B$ 点，因此 $fast$ 指针从 $C$ 点每次走 1 步，$slow$ 指针从原点每次走 1 步，当他们一定会在 $B$ 点相遇并各自走了 $x$ 步

时间复杂度 $O(n)$

时间复杂度分析：$first$ 总共走了 $2x+y$ 步，$second$ 总共走了 $2x+2y+x$ 步，所以两个指针总共走了 $5x+3y$ 步。由于当第一次 $first$ 走到 $b$ 点时，$second$ 最多追一圈即可追上 $first$，所以 $y$ 小于环的长度，所以 $x+y$ 小于等于链表总长度。所以总时间复杂度是 $O(n)$。

参考y总的hh

Java 代码

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public ListNode detectCycle(ListNode head) {
        if(head == null || head.next == null) return null;
        ListNode fast = head.next;
        ListNode slow = head;

        while(fast != null)
        {   
            if(fast == slow) 
            {
                fast = fast.next;
                slow = head;
                while(fast != slow)
                {
                    fast = fast.next;
                    slow = slow.next;
                }
                return slow;
            }
            fast = fast.next;
            if(fast != null) fast = fast.next;
            slow = slow.next;
        }

        return null;
    }
}