题目描述

让我们一起来玩扫雷游戏！

给定一个代表游戏板的二维字符矩阵。 ‘M’ 代表一个未挖出的地雷，’E’ 代表一个未挖出的空方块，’B’ 代表没有相邻（上，下，左，右，和所有4个对角线）地雷的已挖出的空白方块，数字（‘1’ 到 ‘8’）表示有多少地雷与这块已挖出的方块相邻，’X’ 则表示一个已挖出的地雷。

现在给出在所有未挖出的方块中（’M’或者’E’）的下一个点击位置（行和列索引），根据以下规则，返回相应位置被点击后对应的面板：

如果一个地雷（’M’）被挖出，游戏就结束了- 把它改为 ‘X’。
如果一个没有相邻地雷的空方块（’E’）被挖出，修改它为（’B’），并且所有和其相邻的未挖出方块都应该被递归地揭露。
如果一个至少与一个地雷相邻的空方块（’E’）被挖出，修改它为数字（‘1’到‘8’），表示相邻地雷的数量。
如果在此次点击中，若无更多方块可被揭露，则返回面板。

样例

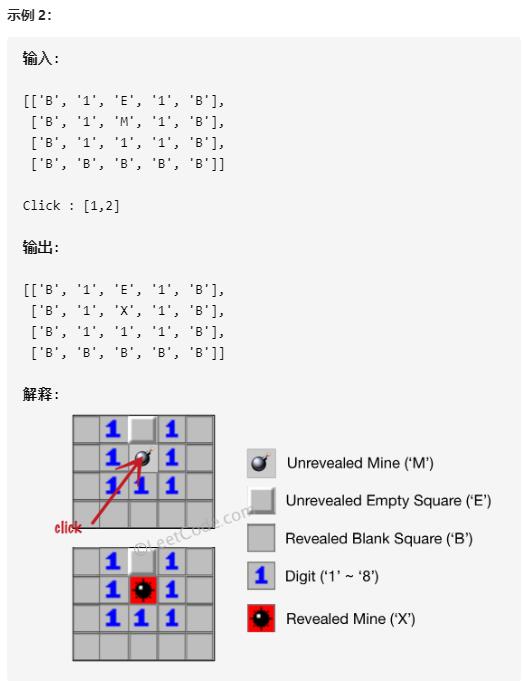
算法

(FloodFill) $O(nm)$

问题分析：根据描述，题目给出的board中，每个位置只可能包含以下元素：

‘M’：代表***，点到了它，把它修改为’X’，其他位置不用管，结束。

‘B’：代表已经被揭露过的空白方块，如果点到它，什么都不用做，结束。

‘1’-‘8’：代表已经被揭露过的数字方块，数值表明它八个方向上的***个数，如果点到它，什么都不用做，结束。

‘E’：没有揭露过的方块，我们要揭露它。揭露它有两种情况，要么是’B’，要么是1’-‘8’.

如果它八个方向的个数大于0，那么它应该被标记为个数。

否则，应该被标记为’B’,按照题目的意思，应该继续递归揭露它八个方向上的方块。进行bfs进行搜索。

C++ 代码

class Solution {
public:
    int dx[8]={1,1,1,0,0,-1,-1,-1},dy[8]={1,0,-1,1,-1,1,0,-1};
    int n,m;
    int num[51][51]={0},st[51][51]={0};
    vector<vector<char>> ans;
    void bfs(int a,int b)
    {
        ans[a][b]='B';
        st[a][b]=true;
        for(int i=0;i<8;i++)
        {
            int x=a+dx[i],y=b+dy[i];
            if(x>=0 && x<n && y>=0 && y<m)
            {
                if(!st[x][y])
                {
                    if(num[x][y]==0) bfs(x,y);
                    else if(num[x][y]==-1) ans[x][y]='X';
                    else ans[x][y]=num[x][y]+'0';
                }
            }
        }
    }
    vector<vector<char>> updateBoard(vector<vector<char>>& board, vector<int>& click) {
        if(board.size()<1) return ans;
        n=board.size(),m=board[0].size();
        ans=board;
        for(int i=0;i<n;i++)
        {
            for(int j=0;j<m;j++)
            {
                if(board[i][j]=='M') num[i][j]=-1;
                else{
                    num[i][j]=0;
                    for(int k=0;k<8;k++)
                    {
                        int x=i+dx[k],y=j+dy[k];
                        if(x>=0 && x<n && y>=0 && y<m && board[x][y]=='M')
                        {
                            num[i][j]++;
                        }
                    }
                }
            }
        }
        int a=click[0],b=click[1];
        st[a][b]=1;
        if(num[a][b]==0)    bfs(a,b);
        else if(num[a][b]==-1) ans[a][b]='X';
        else ans[a][b]=num[a][b]+'0';
        return ans;
    }
};