1、题目中所说的“规定路径都是单向的,且保证都是小序号地窖指向大序号地窖”也就是说，在确定这个点的最大值的时候需要借助的各种能够到达的路径的小序号的点一定是可以确定值的。由此采用动态规划思想进行操作。

2、不同的是初始化，本道题的各个路径的起点不一定相同，而且值是在点上，不再是在路径上，所以如果没有前驱的话（也就是它是一个起点）初始值应该是这个点的值。

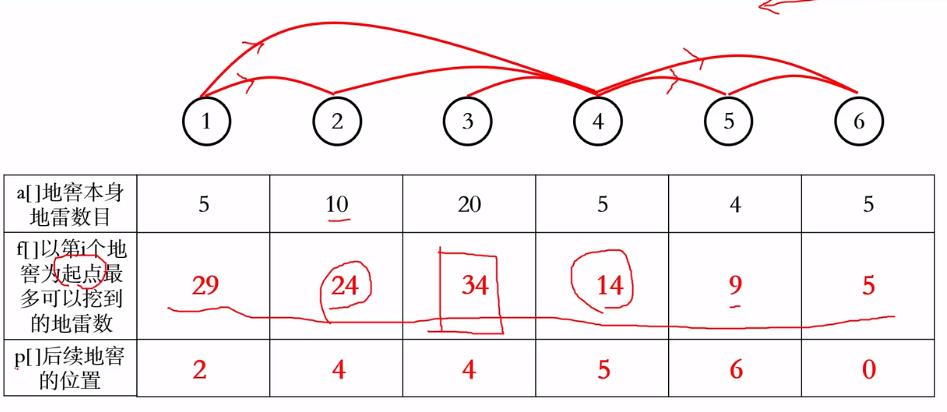
3、本道题中，a[]记录各个点的原本地雷值，g[][]描绘邻接矩阵的二维数组，pre[]记录后续地窖位置，dp[]动态表示每个重点的最优值（一条路径中所遇到的最大的地雷数）

样例：

6
5 10 20 5 4 5
1 2
1 4
2 4
3 4
4 5
4 6
5 6
0 0

样例图解：

C++ 代码

#include<bits/stdc++.h>
using namespace std;
const int N =210;
int g[N][N],a[N];
int dp[N],pre[N];
int main()
{
    memset(g,0,sizeof g);
    int n; scanf("%d",&n);
    for(int i=1;i<=n;i++) scanf("%d",&a[i]);
    int a,b;
    while(scanf("%d%d",&a,&b),a)  //表示当a不为0时一直进行a，b的输入
        g[a][b]=1;
    dp[n]=a[n];         //最后一点不能到任何之前的点，直接赋值为a[n]
    int ans=0,s=0;      //ans为最终答案即地雷数最大的那条路，s为这条路的起点
    for(int i=n-1;i>=1;i--)     //遍历除了最后一点的其他点的情况
    {
        int maxn=0,k=0;     //maxn为第i个点到其他点中地雷数量最多的那个点，k表示其下标
        for(int j=i+1;j<=n;j++)     
        {
            if(g[i][j]==1 && dp[j]>maxn)
            {
                maxn=dp[j];
                k=j;
            }
        }
        dp[i]=a[i]+maxn;
        pre[i]=k;
        if(dp[i]>ans)   
        {
            ans=dp[i];
            s=i;
        }
    }
    while(pre[s]!=0)
    {
        printf("%d-",s);
        s=pre[s];
    }
    printf("%d\n",s);
    printf("%d",ans);
    return 0;
}