题目描述

输入一个n行m列的整数矩阵，再输入q个询问，每个询问包含四个整数x1, y1, x2, y2，表示一个子矩阵的左上角坐标和右下角坐标。

对于每个询问输出子矩阵中所有数的和。

输入格式
第一行包含三个整数n，m，q。

接下来n行，每行包含m个整数，表示整数矩阵。

接下来q行，每行包含四个整数x1, y1, x2, y2，表示一组询问。

输出格式
共q行，每行输出一个询问的结果。

数据范围
1≤n,m≤1000,
1≤q≤200000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤矩阵内元素的值≤1000
输入样例：
3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4
输出样例：
17
27
21

算法1

思路

矩阵前缀和S也就是：

该点到矩阵左上顶点所构成矩形上的所有点和

这里借用一下y总的图。。。QWQ
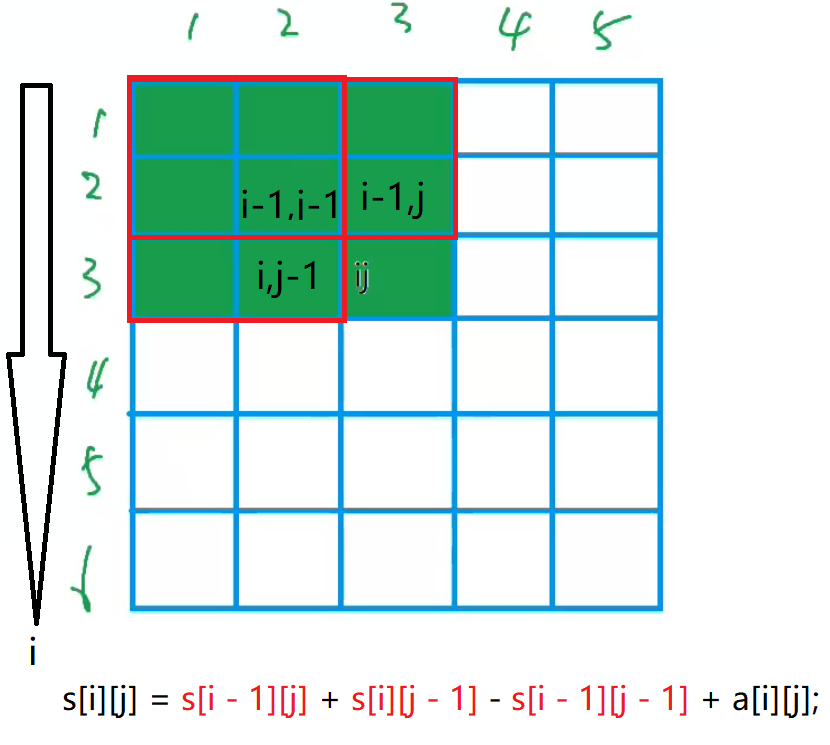
每个点的前缀和：👇

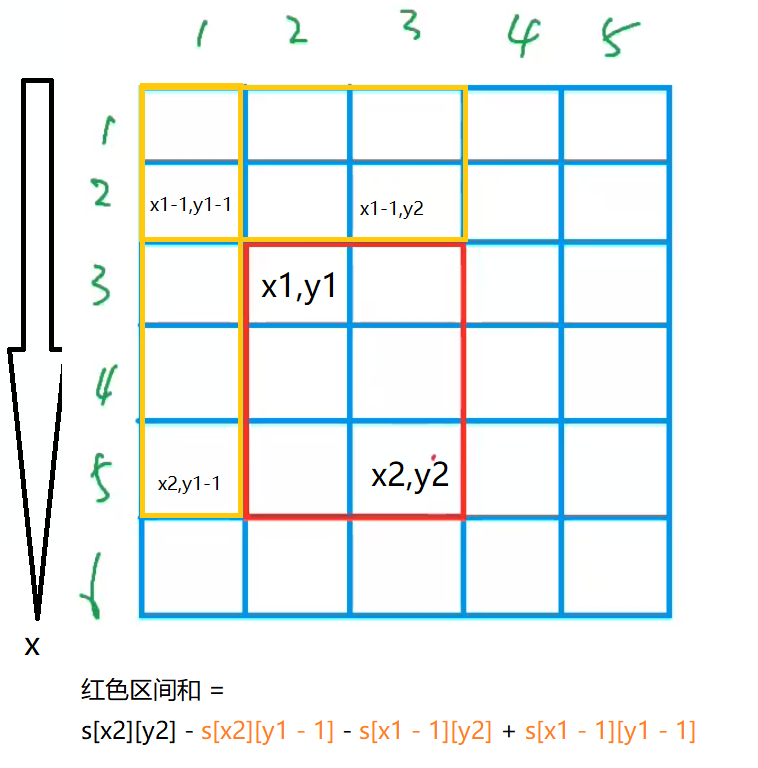
x1,y1,x2,y2所构成矩形区间和：👇

时间复杂度

用前缀和：求前缀和代码一次O(N)，每次查询区间和O(1)
不用前缀和：每次查询区间和都是O(N)

Java 代码

import java.util.Scanner;

public class Main {
    private static int N = 1010;
    private static int[][] a = new int[N][N];
    private static int[][] s = new int[N][N];
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int m = scanner.nextInt();
        int q = scanner.nextInt();
        for(int i = 1; i < n + 1; i++){
            for(int j = 1; j< m + 1; j++){
                a[i][j] = scanner.nextInt();
                //前缀和
                s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];
            }
        }

        while(q-- > 0){
            int x1 = scanner.nextInt();
            int y1 = scanner.nextInt();
            int x2 = scanner.nextInt();
            int y2 = scanner.nextInt();
            System.out.println(s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1]);
        }
    } 
}